Question

【题目】如图，以O为圆心的圆与直线y=﹣x+ 交于A、B两点，若△OAB恰为等边三角形，则弧AB的长度为（ ）

A. π
B.π
C. π
D. π

Answer 1

【答案】C
【解析】解：如图，作OC⊥AB于C，设AB与x轴交于点M，与y轴交于点N．

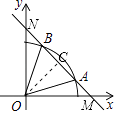
∵直线AB的解析式为y=﹣x+ ，

∴M（ ，0），N（0， ），

∴OM=ON= ，△OMN是等腰直角三角形，

∴∠OMN=∠ONM=45°，

∵OC⊥AB，

∴OC= OM= ．

∵△OAB为等边三角形，OC⊥AB，

∴AB=2AC，AC= = = ，∠AOB=60°，OA=OB=AB，

∴AB= ，

∴弧AB的长度为： = π．

所以答案是：C．

【考点精析】通过灵活运用等边三角形的性质和弧长计算公式，掌握等边三角形的三个角都相等并且每个角都是60°；若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的即可以解答此题．