题目内容
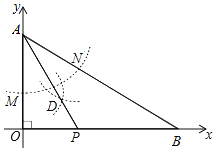
【题目】如图,反比例函数y=![]() (n为常数,n≠0)的图象与一次函数y=kx+8(k为常数,k≠0)的图象在第三象限内相交于点D(﹣
(n为常数,n≠0)的图象与一次函数y=kx+8(k为常数,k≠0)的图象在第三象限内相交于点D(﹣![]() ,m),一次函数y=kx+8与x轴、y轴分别相交于A、B两点.已知cos∠ABO=
,m),一次函数y=kx+8与x轴、y轴分别相交于A、B两点.已知cos∠ABO=![]() .
.
(1)求反比例函数的解析式;
(2)点P是x轴上的动点,当△APC的面积是△BDO的面积的2倍时,求点P的坐标.

【答案】(1)y=![]() x+8,y=
x+8,y=![]() (2)(﹣18,0)或(6,0)
(2)(﹣18,0)或(6,0)
【解析】
(1)求得A(﹣6,0),即可得出一次函数解析式为y=![]() x+8,进而得到D(
x+8,进而得到D(![]() ,﹣2),即可得到反比例函数的解析式为y=
,﹣2),即可得到反比例函数的解析式为y=![]() ;
;
(2)解方程组求得C(![]() ,10),依据△APC的面积是△BDO的面积的2倍,即可得到AP=12,进而得到P(﹣18,0)或(6,0).
,10),依据△APC的面积是△BDO的面积的2倍,即可得到AP=12,进而得到P(﹣18,0)或(6,0).
解:(1)∵一次函数y=kx+8与y轴交于点B,
∴B(0,8).
∵在Rt△AOB中,cos∠ABO=![]() ,
,
∴tan∠BAO=![]() ,
,
∴AO=6,
∴A(﹣6,0).
∵点A在一次函数y=kx+8图象上,
∴k=![]() ,
,
∴一次函数解析式为y=![]() x+8.
x+8.
∵点D(![]() ,m)在一次函数y=kx+8图象上,
,m)在一次函数y=kx+8图象上,
∴m=﹣2,
即D(![]() ,﹣2),
,﹣2),
∵点D(![]() ,﹣2)在反比例函数y=
,﹣2)在反比例函数y=![]() 图象上,
图象上,
∴n=15.
∴反比例函数的解析式为y=![]() ;
;
(2)∵点C是反比例函数y=![]() 图象与一次函数y=
图象与一次函数y=![]() x+8图象的交点,
x+8图象的交点,
∴ ,解得
,解得 ,
,
∴C(![]() ,10).
,10).
∵△APC的面积是△BDO的面积的2倍,
∴![]() AP×10=
AP×10=![]() ×8×
×8×![]() ,
,
∴AP=12,
又∵A(﹣6,0),点P是x轴上的动点,
∴P(﹣18,0)或(6,0).

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目