��Ŀ����
����Ŀ����ѧ������Ϻ������.
��ĸ�к���δ֪���IJ���ʽ�з�ʽ����ʽ.�磺![]() ��
��![]() ��.��ô���������ǵĽ⼯�أ���������ѧ�������������������֪�����������ͬ�ŵ�������ŵø�.����ĸ����ʽΪ��
��.��ô���������ǵĽ⼯�أ���������ѧ�������������������֪�����������ͬ�ŵ�������ŵø�.����ĸ����ʽΪ��
(1)��![]() ��0��
��0��![]() ��0����
��0����![]() ��0����
��0����![]() ��0��
��0��![]() ��0����
��0����![]() ��0��
��0��
(2)��![]() ��0��
��0��![]() ��0����
��0����![]() ��0����
��0����![]() ��0��
��0��![]() ��0����
��0����![]() ��0.
��0.
��֮��(1)��![]() ��0����
��0����![]() ��
��![]()
(2)��![]() ��0����__________��__________.
��0����__________��__________.
(3)�����������ɣ���ʽ![]() �Ľ⼯.
�Ľ⼯.
(4)����ʽ![]() �Ľ⼯.
�Ľ⼯.
���𰸡�![]()
![]()
��������
(2)���������������ŵø����
(3)�ȸ���ͬ�ŵ����Ѳ���ʽת���ɲ���ʽ�飬Ȼ�����һԪһ�β���ʽ��Ľⷨ��⼴��;
(4) �ȸ�����ŵø��Ѳ���ʽת���ɲ���ʽ�飬Ȼ�����һԪһ�β���ʽ��Ľⷨ��⼴��.
��2�������Ķ�������֪����![]() ��0�����ԣ�
��0�����ԣ�![]() ��
��![]() ��ţ�
��ţ�
������![]() ��
��![]() �������.
�������.
��3����![]()
��![]() ���
���![]()
��һԪһ�β���ʽ�飬
�õ���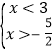 ����
����![]() ��
��
�ɢڵ�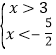 ���⣩
���⣩
�ʲ���ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]()
��4���Բ���ʽ![]() ���������õ���
���������õ���![]() ����
����![]()
�����ɵã�![]()
��![]() ��
��![]()
�ɢٽ��![]() ����
����![]()
�ɢڽ��![]() ����
����![]()
��������������ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]()

��ϰ��ϵ�д�
�����Ŀ