Question

【题目】如图，在四边形ABCD中，AD∥BC，∠ABC=90°，AB=AD，连接BD，点E在AB上，且∠BDE=15°，DE=4，DC=2．

（1）求BE的长；

（2）求四边形DEBC的面积．

（注意：本题中的计算过程和结果均保留根号）

Answer 1

【答案】（1）BE=6﹣2；（2）S四边形DEBC=36+6．

【解析】

（1）解直角三角形求出AD、AE即可解决问题；

（2）作DF⊥BC于F．则四边形ABFD是矩形，解直角三角形求出CF，即可解决问题；

（1）在四边形ABCD中，∵AD∥BC，∠ABC=90°，

∴∠BAD=90°，

∵AB=AD，

∴∠ABD=∠ADB=45°，

∵∠BDE=15°，

∴∠ADE=30°，

在Rt△ADE中，AE=DE×sin30=2，AD=DEcos30°=6，

∴AB=AD=6，

∴BE=6﹣2．

（2）作DF⊥BC于F．则四边形ABFD是矩形，

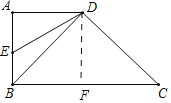
∴BF=AD=6，DF=AB=6，

在Rt△DFC中，FC=，

∴BC=6+4，

∴S四边形DEBC=S△DEB+S△BCD=×（6﹣2）×6+（6+4）×6=36+6．