题目内容
（2003•广西）如图，BD、CE是△ABC的中线，G、H分别是BE、CD的中点，BC=8，求GH的长．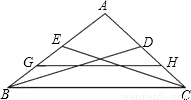
【答案】分析：GH是梯形EBCD的中位线，DE是△ABC的中位线，根据中位线定理就可以求出．
解答：
解法一：连接DE
∵AE=EB，AD=DC
∴DE∥BC，DE=
BC=
×8=4，
又∵EG=GB，DH=HC
∴GH=
（ED+BC）=
（4+8）=6．
解法二：∵E、D分别是AB、AC的中点，G、H分别是EB、DC的中点
∴
，
∴△AGH∽△ABC，
∴
，
∴
．
点评：本题主要考查了三角形的中位线定理，和梯形的中位线定理．
解答：
解法一：连接DE∵AE=EB，AD=DC
∴DE∥BC，DE=
BC=×8=4，又∵EG=GB，DH=HC
∴GH=
（ED+BC）=（4+8）=6．解法二：∵E、D分别是AB、AC的中点，G、H分别是EB、DC的中点
∴
，∴△AGH∽△ABC，
∴
，∴
．点评：本题主要考查了三角形的中位线定理，和梯形的中位线定理．
练习册系列答案
相关题目
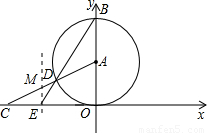
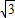）为圆心的圆与x轴相切于坐标原点O，与y轴相交于点B，弦BD的延长线交x轴的负半轴于点E，且∠BEO=60°，AD的延长线交x轴于点C．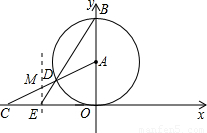
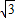）为圆心的圆与x轴相切于坐标原点O，与y轴相交于点B，弦BD的延长线交x轴的负半轴于点E，且∠BEO=60°，AD的延长线交x轴于点C．
