题目内容
二次函数 的图象如图所示,点A位于坐标原点,A1,A2,A3,…,A2009在y轴的正半轴上,B1,B2,B3,…,B2009在二次函数
的图象如图所示,点A位于坐标原点,A1,A2,A3,…,A2009在y轴的正半轴上,B1,B2,B3,…,B2009在二次函数 第一象限的图象上,若△AB1A1,△A1B2A2,△A2B3A3,…,△A2008B2009A2009都为等边三角形,计算出△A2008B2009A2009的边长为 .
第一象限的图象上,若△AB1A1,△A1B2A2,△A2B3A3,…,△A2008B2009A2009都为等边三角形,计算出△A2008B2009A2009的边长为 .
【答案】分析:此题需要从简单的例子入手寻找各三角形边长的规律;可设出△AA1B1的边长为m1,由于此三角形是正三角形,则∠B1AA1=60°,∠B1Ax=30°,可用边长m1表示出B1的坐标,代入抛物线的解析式中,即可得到m1的值,同理可求出△A1B2A2、△A2B3A3的边长,通过观察得到这些三角形边长值的变化规律来求得到△A2008B2009A2009的边长.
解答:解:设△AA1B1的边长为m1;
∵△AA1B1是等边三角形,
∴∠A1AB1=60°,∠B1Ax=30°;
故B1( ,
, );
);
由于点B1在抛物线的图象上,则有:
 ×(
×( m1)2=
m1)2= ,解得m1=1;
,解得m1=1;
同理设△A1A2B2的边长为m2;
同上可得B2( ,1+
,1+ );
);
由于点B2也在抛物线的图象上,则有:
 ×(
×( m2)2=
m2)2= +1,解得m2=2;
+1,解得m2=2;
依此类推,△A2B3A3的边长为:m3=3,
…
△AnBn+1An+1的边长为mn+1=n+1;
∴△A2008B2009A2009的边长为2009.
点评:此题是典型的规律型试题,需要从简单的例子入手来找出题目的一般化规律,然后根据得到的规律求出特定的值.
解答:解:设△AA1B1的边长为m1;
∵△AA1B1是等边三角形,
∴∠A1AB1=60°,∠B1Ax=30°;
故B1(
 ,
, );
);由于点B1在抛物线的图象上,则有:
 ×(
×( m1)2=
m1)2= ,解得m1=1;
,解得m1=1;同理设△A1A2B2的边长为m2;
同上可得B2(
 ,1+
,1+ );
);由于点B2也在抛物线的图象上,则有:
 ×(
×( m2)2=
m2)2= +1,解得m2=2;
+1,解得m2=2;依此类推,△A2B3A3的边长为:m3=3,
…
△AnBn+1An+1的边长为mn+1=n+1;
∴△A2008B2009A2009的边长为2009.
点评:此题是典型的规律型试题,需要从简单的例子入手来找出题目的一般化规律,然后根据得到的规律求出特定的值.

练习册系列答案
相关题目
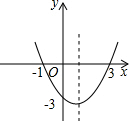 已知二次函数的图象如图所示,则这个二次函数的表达式为( )
已知二次函数的图象如图所示,则这个二次函数的表达式为( )| A、y=x2-2x+3 | B、y=x2-2x-3 | C、y=x2+2x-3 | D、y=x2+2x+3 |
 16、已知二次函数的图象如图所示,则
16、已知二次函数的图象如图所示,则 21、已知二次函数的图象如图所示,求它的解析式.
21、已知二次函数的图象如图所示,求它的解析式. 二次函数的图象如图所示,P为图象顶点,A为图象与y轴交点.
二次函数的图象如图所示,P为图象顶点,A为图象与y轴交点. 二次函数的图象如图所示,则a
二次函数的图象如图所示,则a