Question

【题目】平面直角坐标系xOy中，对称轴平行于y轴的抛物线过点A（1，0）、B（3，0）和C（4，6）；

（1）求抛物线的表达式；

（2）现将此抛物线先沿x轴方向向右平移6个单位，再沿y轴方向平移k个单位，若所得抛物线与x轴交于点D、E（点D在点E的左边），且使△ACD∽△AEC（顶点A、C、D依次对应顶点A、E、C），试求k的值，并注明方向．

Answer 1

【答案】（1）y=2x2﹣8x+6；（2）向下平移6个单位．

【解析】试题分析：（1）利用待定系数法直接求出抛物线的解析式；

（2）设出D，E坐标，根据平移，用k表示出平移后的抛物线解析式，利用坐标轴上点的特点得出m+n=16，mn=63﹣，进而利用相似三角形得出比例式建立方程即可求出k．

试题解析：解：（1）∵抛物线过点A（1，0）、B（3，0），∴设抛物线的解析式为y=a（x﹣1）（x﹣3）。

∵C（4，6），∴6=a（4﹣1）（4﹣3），∴a=2，∴抛物线的解析式为y=2（x﹣1）（x﹣3）=2x2﹣8x+6；

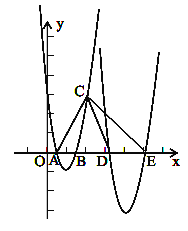
（2）如图，设点D（m，0），E（n，0）。

∵A（1，0），∴AD=m﹣1，AE=n﹣1。

由（1）知，抛物线的解析式为y=2x2﹣8x+6=2（x﹣2）2﹣2，∴将此抛物线先沿x轴方向向右平移6个单位，得到抛物线的解析式为y=2（x﹣8）2﹣2，∴再沿y轴方向平移k个单位，得到的抛物线的解析式为y=2（x﹣8）2﹣2﹣k。

令y=0，则2（x﹣8）2﹣2﹣k=0，∴2x2﹣32x+126﹣k=0。

根据根与系数的关系得：∴m+n=16，mn=63﹣。

∵A（1，0），C（4，6），∴AC2=（4﹣1）2+62=45。

∵△ACD∽△AEC，∴ ，∴AC2=ADAE，∴45=（m﹣1）（n﹣1）=mn﹣（m+n）+1，

∴45=63﹣﹣16+1，∴k=6，即：k=6，向下平移6个单位．