题目内容
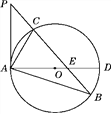
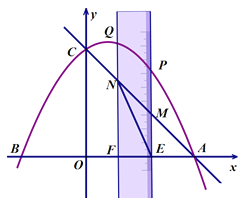
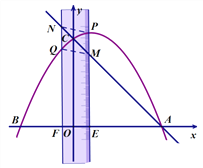
【题目】如图，已知抛物线
与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，有一宽度为1的刻度尺沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和点Q，交直线AC于点M和点N，交x轴于点E和点F．
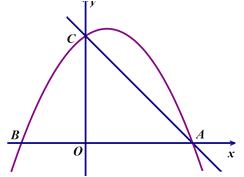
（1）求点A、B、C的坐标；
（2）当点M和点N都在线段AC上时，连接EN，如果点E的坐标为（4，0），求sin∠ANE的值；
（3）在刻度尺平移过程中，当以点P、Q、N、M为顶点的四边形是平行四边形时，求点N的坐标．
【答案】（1）A（5，0）、B（-3，0）、C（0，5）;(2) 
;(3) 点N的坐标为（2，3）或（2+
，3﹣
）或（2﹣
，3+
）
【解析】（1）令y=0得： 
=0，解得x=5或x=-3．
∵点A在点B的右侧，
∴点A、B的坐标分为（5，0）、（-3，0）．
当x=0时，y=5，
∴点C的坐标为（0，5）．………………………………………………3分
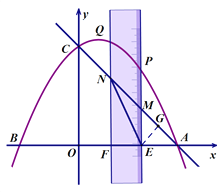（2）如图1，作EG⊥AC，垂足为点G．
∵点E的坐标为（4，0），
∴OE=4．
∵OA=OC=5，
∴AE=1，∠OAC=45°．
∴AF=FN=2，GE=AEsin45°=
．………………5分
在Rt△EFN中，依据勾股定理可知NE=
=
=
．………………6分
∴sin∠ANE=
=
=
．……………………7分
（3）设直线AC的函数表达式为y=kx+b．
将点A和点C的坐标代入得： 
，
解得k=﹣1，b=5．
∴直线AC的函数表达式为y=﹣x+5．………………9分
①当MN为边时，如图2所示：
设点Q（n， 
），则点P（n+1， 
），点N（n，﹣n+5）M(n+1，-n+4)．
∵QN=PM
∴
，解得n=2．
∴点N的坐标为（2，3）．………………………………10分
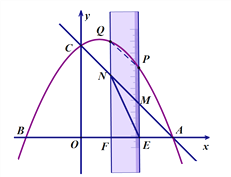
当MN是平行四边形的对角线时，如图3所示：
设点F的坐标为（m，0），
则N（m，﹣m+5），M（m+1，﹣m+4）,
Q（m， 
），P（m+1， 
）．
∵QN = PM，
∴
，解得m=2±
．
∴点N的坐标为（2
，3﹣）或（2﹣，3+）．
综上所述，以点P、Q、N、M为顶点的四边形是平行四边形时，点N的坐标为（2，3）或（2，3﹣）或（2﹣，3+
）．…………………………12分
