题目内容
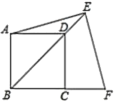
【题目】如图,正方形![]() 中,点
中,点![]() 为射线
为射线![]() 上一点,
上一点,![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,则
,则![]() ______
______
【答案】![]()
【解析】
连接AC交BD于O,作FG⊥BE于G,证出△BFG是等腰直角三角形,得出BG=FG=![]() BF=
BF=![]() ,由三角形的外角性质得出∠AED=30°,由直角三角形的性质得出OE=
,由三角形的外角性质得出∠AED=30°,由直角三角形的性质得出OE=![]() OA,求出∠FEG=60°,∠EFG=30°,进而求出OA的值,即可得出答案.
OA,求出∠FEG=60°,∠EFG=30°,进而求出OA的值,即可得出答案.
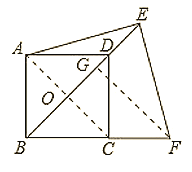
连接AC交BD于O,作FG⊥BE于G,如图所示
则∠BGF=∠EGF=90°
∵四边形ABCD是正方形
∴AC⊥BD,OA=OB=OC=OD,∠ADB=∠CBG=45°
∴△BFG是等腰直角三角形
∴BG=FG=![]() BF=
BF=![]()
∵∠ADB=∠EAD+∠AED,∠EAD=15°
∴∠AED=30°
∴OE=![]() OA
OA
∵EF⊥AE
∴∠FEG=60°
∴∠EFG=30°
∴EG=![]() FG=
FG=![]()
∴BE=BG+EG=![]()
∵OA+![]() AO=
AO=![]()
解得:OA=![]()
∴AB=![]() OA=
OA=![]()
故答案为![]()

 备战中考寒假系列答案
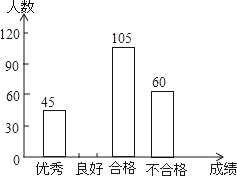
备战中考寒假系列答案【题目】为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
【题目】某商店销售一种商品,每件成本8元,规定每件商品售价不低于成本,且不高于20元,经市场调查每天的销售量y(件)与每件售价x(元)满足一次函数关系,部分数据如下表:
售价x(元件) | 10 | 11 | 12 | 13 | 14 | x |
销售量y(件) | 100 | 90 | 80 | 70 |
|
|
(1)将上面的表格填充完整;
(2)设该商品每天的总利润为w元,求w与x之间的函数表达式;
(3)计算(2)中售价为多少元时,获得最大利润,最大利润是多少?