Question

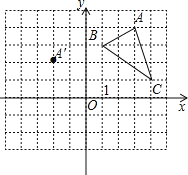
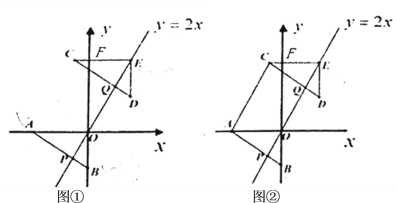
【题目】如图①，在平面直角坐标系中，点，的坐标分别为，，点在直线上，将沿射线方向平移，使点与点重合，得到（点、分别与点、对应），线段与轴交于点，线段，分别与直线交于点，．

（1）求点的坐标；

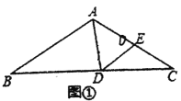
（2）如图②，连接，四边形的面积为__________（直接填空）；

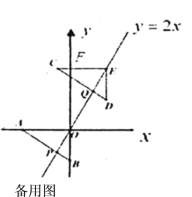
（3）过点的直线与直线交于点，当时，请直接写出点的坐标．

Answer 1

【答案】（1）C（-1,6）；（2）24；（3）点N的坐标为（，）或（， ）；

【解析】

（1）先求出点E的坐标，根据平移得到OA=CE=4，即可得到点C的坐标；

（2）根据图象平移得到四边形的面积等于的面积，根据面积公式计算即可得到答案；

（3）根据直线特点求出，tan∠NCE=tan∠POB=，再分两种情况：点N在CE的上方或下方时，分别求出直线CN的解析式得到点N的坐标即可.

（1）∵点在直线上，

∴m=6，

∴E（3,6），

由平移得CE=OA=4，

∴点C的坐标是（-1,6）；

（2）由平移得到四边形的面积等于的面积，

∴，

故答案为：24；

（3）由直线y=2x得到：tan∠POB=，

当时，tan∠NCE=tan∠POB=，

①当点N在CE上方时，直线CE的表达式为：，

低昂点C的坐标代入上式并解得：b=，

∴直线CN的表达式是y=x+，

将上式与y=2x联立并解得：x=，y=，

∴N（，）；

②当点N在CE下方时，直线CE的表达式为：y=-x+，

同理可得：点N（， ）；

综上，点N的坐标为（，）或（， ）.