Question

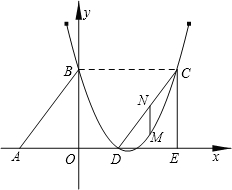
如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（，0）、（0，4），抛物线经过B点，且顶点在直线上．

【小题1】（1）求抛物线对应的函数关系式；
【小题2】（2）若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；
【小题3】（3）若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为l．求l与t之间的函数关系式，并求l取最大值时，点M的坐标．

Answer 1

【小题1】（1）由题意，可设所求抛物线对应的函数关系式为 
∴
∴    
∴所求函数关系式为：
【小题2】（2）在Rt△ABO中，OA=3，OB=4，
∴
∵四边形ABCD是菱形
∴BC=CD=DA=AB="5   "
∴C、D两点的坐标分别是（5，4）、（2，0）． 
当时，
当时，
∴点C和点D在所求抛物线上
【小题3】（3）设直线CD对应的函数关系式为，则

解得：．
∴      
∵MN∥y轴，M点的横坐标为t，
∴N点的横坐标也为t．
则， ，
∴
∵，∴当时，，
此时点M的坐标为（，）．

解析