题目内容
【题目】如图,点![]() 是直线
是直线![]() 与
与![]() 的交点,点
的交点,点![]() 在
在![]() 上,
上, ![]() 垂足为
垂足为![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() .
.
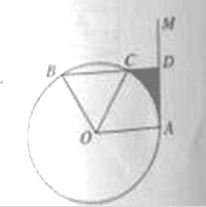
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求图中阴影部分的面积(结果保留
,求图中阴影部分的面积(结果保留![]() 和根号).
和根号).
【答案】(1)见解析;(2)![]() .
.
【解析】
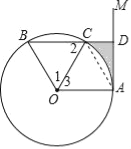
试题分析:(1)由已知条件得到△BOC是等边三角形,根据等边三角形的性质得到∠1=∠2=60°,由角平分线的性质得到∠1=∠3,根据平行线的性质得到∠OAM=90°,于是得到结论;
(2)根据等边三角形的性质得到∠OAC=60°,根据三角形的内角和得到∠CAD=30°,根据勾股定理得到AD=2![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)∵∠B=60°,∴△BOC是等边三角形,∴∠1=∠2=60°,
∵OC平分∠AOB,∴∠1=∠3,∴∠2=∠3,∴OA∥BD,
∴∠BDM=90°,∴∠OAM=90°,∴AM是⊙O的切线;
(2)∵∠3=60°,OA=OC,∴△AOC是等边三角形,
∴∠OAC=60°,∵∠OAM=90°,∴∠CAD=30°,
∵CD=2,∴AC=2CD=4,∴AD=2![]() ,
,
∴S阴影=S梯形OADC﹣S扇形OAC=![]() (4+2)×2
(4+2)×2![]() ﹣
﹣![]() .
.

练习册系列答案
相关题目