题目内容
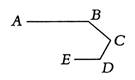
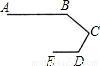
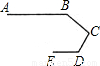
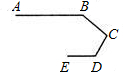如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=140°，∠D=120°，则∠C的度数为________度．
100
分析：过点C作CF∥AB，由平行线性质可得∠B，∠D，∠BCF，∠DCF的关系，进而求得∠C．
解答：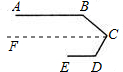
解：如图所示：过点C作CF∥AB．
∵AB∥DE，
∴DE∥CF；
∴∠BCF=180°-∠B=40°，∠DCF=180°-∠D=60°；
∴∠C=∠BCF+∠DCF=100°．
故填100．
点评：本题运用了两直线平行，同旁内角互补的性质，需要作辅助线求解，难度中等．
分析：过点C作CF∥AB，由平行线性质可得∠B，∠D，∠BCF，∠DCF的关系，进而求得∠C．
解答：
解：如图所示：过点C作CF∥AB．∵AB∥DE，
∴DE∥CF；
∴∠BCF=180°-∠B=40°，∠DCF=180°-∠D=60°；
∴∠C=∠BCF+∠DCF=100°．
故填100．
点评：本题运用了两直线平行，同旁内角互补的性质，需要作辅助线求解，难度中等．
练习册系列答案
相关题目
17、如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=140°，∠D=120°，则∠C的度数为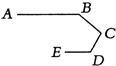
5、如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=140°，∠D=120°，则∠C的度数为（ ）
