Question

本题10分)

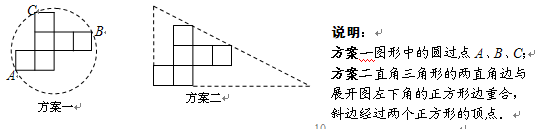
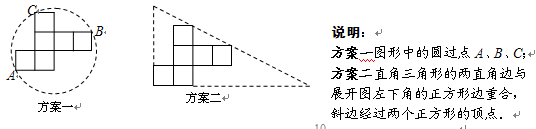
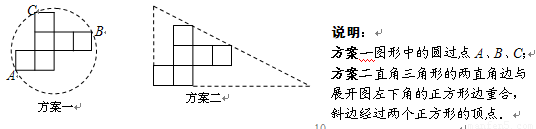
 操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的圆形纸片进行如下设计：

 

纸片利用率=×100%

 

发现：（1）方案一中的点A、B恰好为该圆一直径的两个端点．你认为小明的这个发现是否正确，请说明理由．

（2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．

  探究：（3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．

 

Answer 1

解：（1）小明的这个发现正确．说明∠ACB=90°                （3分）

 （2） 37.5%．                                             （4分）

（3）                                                 （3分）

 

解析:解：（1）小明的这个发现正确．

理由：如图1：连接AC、BC、AB，

∵AC=BC=，AB=

∴AC²+BC²=AB²，

∴∠ACB=90°，

∴AB为该圆的直径．

（2）由题意，可得△ADE≌△EHF（ASA），

∴AD=EH=1．

∵DE∥BC，

∴△ADE∽△ACB，

∴=，

∴=，

∴BC=8．

∴S△ACB=16．

∴该方案纸片利用率=×100%=37.5%．

∴37.5%＜38.2%，