题目内容
【题目】已知：如图，抛物线y＝﹣x2+2x+3交x轴于点A、B，其中点A在点B的左边，交y轴于点C，点P为抛物线上位于x轴上方的一点．
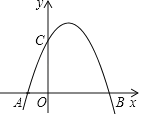
（1）求A、B、C三点的坐标；
（2）若△PAB的面积为4，求点P的坐标．
【答案】（1）A（﹣1，0），B（3，0），C（0，3）；（2）P点坐标为（1﹣
，2），（1+，2）
【解析】
（1）当
时，可求点A，点B坐标，当
，可求点C坐标；
（2）设点P的纵坐标为
，利用三角形面积公式可求得
，代入y=﹣x2+2x+3即可求得点P的横坐标，从而求得答案.
（1）对于抛物线y=﹣x2+2x+3，
令y=0，得到﹣x2+2x+3=0，
解得：x1=﹣1，x2=3，
则A（﹣1，0），B（3，0），
令，得到y=﹣x2+2x+3=3，
则C点坐标为（0，3）；
故答案为：A（﹣1，0），B（3，0），（0，3）；
（2）设点P的纵坐标为，
∵点P为抛物线上位于x轴上方，
∴
，
∵△PAB的面积为4，
∴
，
解得：
，
∵点P为抛物线上的点，
将代入y=﹣x2+2x+3得：﹣x2+2x+3=2，
整理得x2﹣2x﹣1=0，
解得：x1=1﹣
，x2=1+，
∴P点坐标为：（1﹣，2），（1+，2）．
练习册系列答案
相关题目
【题目】重庆八中某数学兴趣小组同学探究函数
的图象与性质，根据学习函数的经验，该小组进行了系列探究．
下表给出了自变量
与函数
的一些对应值：
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| … | 2 | 3 | 4 |
|
| 1 |
| … |
（1）补全表格：
，
；
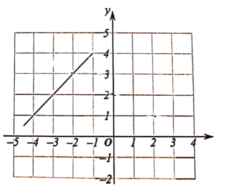
（2）在如图所示的面直角坐标系中，补全函数的图象并写出该函数的一条性质：
____________________________________________________________________________；
（3）若函数
，直接写出不等式
的解集．
