题目内容
【题目】 如图,在菱形![]() 中,点
中,点![]() 在对角线
在对角线![]() 上,且
上,且![]() ,
,![]() 是
是![]() 的外接圆.
的外接圆.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 求
求![]() 的半径.
的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
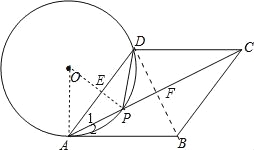
试题分析:(1)连结OP、OA,OP交AD于E,由PA=PD得弧AP=弧DP,根据垂径定理的推理得OP⊥AD,AE=DE,则∠1+∠OPA=90°,而∠OAP=∠OPA,所以∠1+∠OAP=90°,再根据菱形的性质得∠1=∠2,所以∠2+∠OAP=90°,然后根据切线的判定定理得到直线AB与⊙O相切;
(2)连结BD,交AC于点F,根据菱形的性质得DB与AC互相垂直平分,则AF=4,tan∠DAC=![]() ,得到DF=2
,得到DF=2![]() ,根据勾股定理得到AD=
,根据勾股定理得到AD=![]() =2
=2![]() ,求得AE=
,求得AE=![]() ,设⊙O的半径为R,则OE=R﹣
,设⊙O的半径为R,则OE=R﹣![]() ,OA=R,根据勾股定理列方程即可得到结论.
,OA=R,根据勾股定理列方程即可得到结论.
试题解析:(1)连结OP、OA,OP交AD于E,如图,
∵PA=PD,
∴弧AP=弧DP,
∴OP⊥AD,AE=DE,
∴∠1+∠OPA=90°,
∵OP=OA,
∴∠OAP=∠OPA,
∴∠1+∠OAP=90°,
∵四边形ABCD为菱形,
∴∠1=∠2,
∴∠2+∠OAP=90°,
∴OA⊥AB,
∴直线AB与⊙O相切;
(2)连结BD,交AC于点F,如图,
∵四边形ABCD为菱形,
∴DB与AC互相垂直平分,
∵AC=8,tan∠BAC=![]() ,
,
∴AF=4,tan∠DAC=![]() =
=![]() ,
,
∴DF=2![]() ,
,
∴AD=![]() =2
=2![]() ,
,
∴AE=![]() ,
,
在Rt△PAE中,tan∠1=![]() =
=![]() ,
,
∴PE=![]() ,
,
设⊙O的半径为R,则OE=R﹣![]() ,OA=R,
,OA=R,
在Rt△OAE中,∵OA2=OE2+AE2,
∴R2=(R﹣![]() )2+(
)2+(![]() )2,
)2,
∴R=![]() ,
,
即⊙O的半径为![]() .
.

【题目】甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
次数 运动员 环数 | 1 | 2 | 3 | 4 | 5 |
甲 | 10 | 8 | 9 | 10 | 8 |
乙 | 10 | 9 | 9 | a | b |
某同学计算出了甲的成绩平均数是9,方差是![]() ,请作答:
,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙的射击成绩平均数都一样,则![]() ;
;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出![]() 的所有可能取值,并说明理由.
的所有可能取值,并说明理由.

【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间 (小时) | 频数 (人) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
频数分布直方图
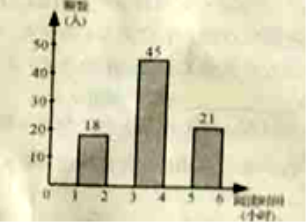
(1)填空:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由![]() 名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.