题目内容
如图，AF平分∠BAC，D是射线AC上一点，DE∥AB交AF于点E，如果∠CDE=50°，则∠DEA=________．
25°
分析：由两直线平行，同位角相等，得∠CDE=∠CAB=50°，再根据角平分线的性质得：∠CAF=∠BAF=25°，最后根据两直线平行，内错角相等得∠DEA=25°．
解答：∵DE∥AB，∠CDE=50°，
∴∠CAB=∠CDE=50°，∠DEA=∠FAB，
∵AF平分∠BAC，
∴∠FAB=
∠CAB=25°．
故答案为：25°．
点评：此题考查了平行线的性质与角平分线的性质．此题比较简单，注意掌握两直线平行，同位角相等与两直线平行，内错角相等定理的应用．
分析：由两直线平行，同位角相等，得∠CDE=∠CAB=50°，再根据角平分线的性质得：∠CAF=∠BAF=25°，最后根据两直线平行，内错角相等得∠DEA=25°．
解答：∵DE∥AB，∠CDE=50°，
∴∠CAB=∠CDE=50°，∠DEA=∠FAB，
∵AF平分∠BAC，
∴∠FAB=
∠CAB=25°．故答案为：25°．
点评：此题考查了平行线的性质与角平分线的性质．此题比较简单，注意掌握两直线平行，同位角相等与两直线平行，内错角相等定理的应用．
练习册系列答案
相关题目
26、已知：如图，CD是△ABC外角∠MCA的平分线，CD与三角形的外接圆交于点D．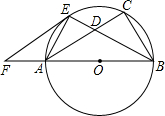
⊙O于E，过E作EF∥AC交BA的延长线于F．AF=5，EF=10，
20、如图，在平行四边形ABCD中，∠BAD和∠BCD的平分线分别交DC、BA的延长线于点F、E．试说明AF=CE．
如图，在平行四边形ABCD中，E是AD的中点，CE交BA的延长线于点F．
；
与AB三者之间的数量关系，并证明你的猜想；