题目内容
如图:长方形ABCD中,AD=10,AB=4,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为 .

2或2.5或3或8.
【解析】
试题分析:∵AD=10,点Q是BC的中点,∴BQ= BC=
BC= ×10=5,
×10=5,
如图1,PQ=BQ=5时,过点P作PE⊥BC于E,

根据勾股定理,QE= ,
,
∴BE=BQ﹣QE=5﹣3=2,∴AP=BE=2;
②如图2,BP=BQ=5时,过点P作PE⊥BC于E,

根据勾股定理,BE= ,∴AP=BE=3;
,∴AP=BE=3;
③如图3,PQ=BQ=5且△PBQ为钝角三角形时,

BE=QE+BQ=3+5=8,AP=BE=8,
④若BP=PQ,如图4,过P作PE⊥BQ于E,则BE=QE=2.5,∴AP=BE=2.5.
综上所述,AP的长为2或3或8或2.5.
故答案为:2或3或8或2.5.

考点:1.等腰三角形的判定;2.勾股定理;3.矩形的性质;4.分类讨论.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 B.
B. 与
与 C.
C. 与
与 D.
D. 与
与
 的图象上有两点(3,a)和(-5,a),则此拋物线的对称轴是( )
的图象上有两点(3,a)和(-5,a),则此拋物线的对称轴是( ) B.直线
B.直线 C.直线
C.直线 D.直线
D.直线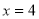



 (其中k为常数),分别取x1=-0.99、x2=0.98、x3=0.99时对应的函数值分别为y1, y2, y3,请将y1, y2, y3用“<”连接起来__ __.
(其中k为常数),分别取x1=-0.99、x2=0.98、x3=0.99时对应的函数值分别为y1, y2, y3,请将y1, y2, y3用“<”连接起来__ __.