题目内容
【题目】如图，
的直径
，半径
，
为
上一动点（不包括
两点），
，垂足分别为
．
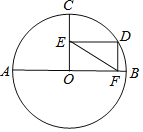
（1）求
的长．
（2）若点
为
的中点，
①求劣弧
的长度，
②者点
为直径
上一动点，直接写出
的最小值．
【答案】（1）
（2）①
②
【解析】
（1）求出圆的半径，再判断出四边形OFDE是矩形，然后根据矩形的对角线相等解答即可；
（2）①根据线段中点的定义得到OE=
OC=OD，根据三角形的内角和得到∠DOE=60°，于是得到结论；
②延长CO交⊙O于G，连接DG交AB于P，则PC+PD的最小值等于DG长，解直角三角形即可得到结论．
解：（1）如图，连接
，
∵
的直径
，
∴圆的半径为
.
∵
，
∴四边形
是矩形，
∴
.
（2）①∵点
为
的中点，
∴
，
∴
，
∴
，
∴劣弧
的长度为
.
②.
延长
交于点
，连接
交
于点
，
则
的最小值为.
∵
，
，
∴
，
∴的最小值为.
阅读快车系列答案
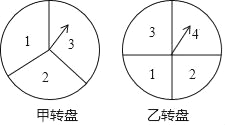
【题目】如图，甲分为三等分数字转盘，乙为四等分数字转盘，自由转动转盘．
（1）转动甲转盘，指针指向的数字小于3的概率是 ；
（2）同时自由转动两个转盘，用列举的方法求两个转盘指针指向的数字均为奇数的概率．
【题目】在大课间活动中，体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试，并对成绩进行统计分析，绘制了频数分布表和统计图，请你根据图表中的信息完成下列问题：
分 组 | 频数 | 频率 |
第一组（0≤x＜15） | 3 | 0.15 |
第二组（15≤x＜30） | 6 | a |
第三组（30≤x＜45） | 7 | 0.35 |
第四组（45≤x＜60） | b | 0.20 |
（1）频数分布表中a=_____，b=_____，并将统计图补充完整；
（2）如果该校七年级共有女生180人，估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人？
（3）已知第一组中只有一个甲班学生，第四组中只有一个乙班学生，老师随机从这两个组中各选一名学生谈心得体会，则所选两人正好都是甲班学生的概率是多少？
