题目内容
(2013•宿迁)在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
分析:如图,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,可得四边形CDPE是正方形,则CD=DP=PE=EC;等腰Rt△ABC中,∠C=90°,AC=1,所以,可求出AC=1,AB=
,又AB=AP;所以,在直角△AEP中,可运用勾股定理求得DP的长即为点P到BC的距离.
| 2 |
解答:解:①如图,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,
∵CP∥AB,
∴∠PCD=∠CBA=45°,
∴四边形CDPE是正方形,
则CD=DP=PE=EC,
∵在等腰直角△ABC中,AC=BC=1,AB=AP,
∴AB=
=
,
∴AP=
;
∴在直角△AEP中,(1+EC)2+EP2=AP2
∴(1+DP)2+DP2=(
)2,
解得,DP=
;
②如图,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,
同理可证,四边形CDPE是正方形,
∴CD=DP=PE=EC,
同理可得,在直角△AEP中,(EC-1)2+EP2=AP2,
∴(PD-1)2+PD2=(
)2,
解得,PD=
;
故选D.
∵CP∥AB,
∴∠PCD=∠CBA=45°,
∴四边形CDPE是正方形,

则CD=DP=PE=EC,
∵在等腰直角△ABC中,AC=BC=1,AB=AP,
∴AB=
| 12+12 |
| 2 |
∴AP=
| 2 |
∴在直角△AEP中,(1+EC)2+EP2=AP2
∴(1+DP)2+DP2=(
| 2 |
解得,DP=
| ||
| 2 |
②如图,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,

同理可证,四边形CDPE是正方形,
∴CD=DP=PE=EC,
同理可得,在直角△AEP中,(EC-1)2+EP2=AP2,
∴(PD-1)2+PD2=(
| 2 |
解得,PD=
| ||
| 2 |
故选D.
点评:本题考查了勾股定理的运用,通过添加辅助线,可将问题转化到直角三角形中,利用勾股定理解答;考查了学生的空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
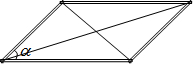 (2013•宿迁)如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为
(2013•宿迁)如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为