题目内容
⊙O的弦AB的长为24cm，弦AB的弦心距为5cm，则⊙O的直径为________．
26cm
分析：根据题意画出相应的图形，连接OA，由OC为弦心距得到OC垂直于AB，利用垂径定理得到C为AB的中点，求出AC的长，在直角三角形AOC中，由OC与AC的长，利用勾股定理求出OA的长，即可得到圆O的直径长．
解答：
解：根据题意画出相应的图形，连接OA，如图所示，
∵OC为AB的弦心距，
∴OC⊥AB，又AB=24cm，
∴C为AB的中点，即AC=BC=
AB=12cm，
在Rt△AOC中，OC=5cm，AC=12cm，
根据勾股定理得：OA=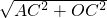
=13cm，
则AB=2AC=26cm．
故答案为：26cm
点评：此题考查了垂径定理，以及勾股定理，熟练掌握定理是解本题的关键．
分析：根据题意画出相应的图形，连接OA，由OC为弦心距得到OC垂直于AB，利用垂径定理得到C为AB的中点，求出AC的长，在直角三角形AOC中，由OC与AC的长，利用勾股定理求出OA的长，即可得到圆O的直径长．
解答：
解：根据题意画出相应的图形，连接OA，如图所示，∵OC为AB的弦心距，
∴OC⊥AB，又AB=24cm，
∴C为AB的中点，即AC=BC=
AB=12cm，在Rt△AOC中，OC=5cm，AC=12cm，
根据勾股定理得：OA=
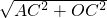=13cm，则AB=2AC=26cm．
故答案为：26cm
点评：此题考查了垂径定理，以及勾股定理，熟练掌握定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
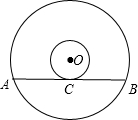如图，是一张电脑光盘的表面，两个圆心都是O，大圆的弦AB所在的直线是小圆的切线，切点为C，已知大圆的半径为5cm，小圆的半径为1cm，则弦AB的长是多少？
（2013•昆山市二模）在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y=x的图象被⊙P截得的弦AB的长为
如图，⊙O的直径AB与弦AC的夹角是30°，过点C作⊙O的切线交AB的延长线于点D，若OD=24cm，则⊙O的直径AB的长为
（2013•黄浦区二模）如图，MN是⊙O的直径，点A是弧
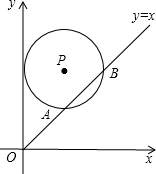如图，在平面直角坐标系中，⊙P的圆心是（