Question

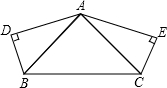如图，已知AB=AC，AD=AE，∠ADB=∠AEC=Rt∠，则∠DBC=∠ECB．请说明理由．

Answer 1

分析：首先根据等腰三角形的性质，得出∠ABC=∠ACB．再根据直角三角形的全等判定，证明Rt△ADB≌Rt△AEC，进而得出∠ADB=∠ACE．最后根据三角形角间的关系，得出结论．

解答：证明：∵AB=AC
∴∠ABC=∠ACB
在Rt△ADB与Rt△AEC中

AB=AC AD=AE

?Rt△ADB≌Rt△AEC?∠ADB=∠ACE
∴∠ABC+∠ADB=∠ACB+∠ACE
又∵∠DBC=∠ABC+∠ADB，∠ECB=∠ACB+∠ACE
∴∠DBC=∠ECB

点评：本题考查全等三角形的性质、等腰三角形的性质、直角三角形的判定．