题目内容
若一次函数y=(1-2k)x-k的函数值y随x的增大而增大,且此函数的图象经过第一、三、四象限,则k的取值范围是
- A.k<

- B.

- C.

- D.0<k<

D
分析:若函数y随x的增大而增大,则1-2k>0;函数的图象经过一、三、四象限,则-k<0;最后解两个不等式确定k的范围.
解答:根据一次函数的性质,函数y随x的增大而增大,
则1-2k>0,
解得k< ;
;
函数的图象经过一、三、四象限,说明图象与y轴的交点在x轴下方,即-k<0,
解得:k>0;
所以k的取值范围为:0<k< .
.
故选:D.
点评:此题主要考查了一次函数图象与系数的关系,同学们应熟练掌握一次函数y=kx+b的性质.当k>0,y随x的增大而增大,图象一定过第一、三象限;当k<0,y随x的增大而减小,图象一定过第二、四象限;当b>0,图象与y轴的交点在x轴上方;当b=0,图象过原点;当b<0,图象与y轴的交点在x轴下方.
分析:若函数y随x的增大而增大,则1-2k>0;函数的图象经过一、三、四象限,则-k<0;最后解两个不等式确定k的范围.
解答:根据一次函数的性质,函数y随x的增大而增大,
则1-2k>0,
解得k<
 ;
;函数的图象经过一、三、四象限,说明图象与y轴的交点在x轴下方,即-k<0,
解得:k>0;
所以k的取值范围为:0<k<
 .
.故选:D.
点评:此题主要考查了一次函数图象与系数的关系,同学们应熟练掌握一次函数y=kx+b的性质.当k>0,y随x的增大而增大,图象一定过第一、三象限;当k<0,y随x的增大而减小,图象一定过第二、四象限;当b>0,图象与y轴的交点在x轴上方;当b=0,图象过原点;当b<0,图象与y轴的交点在x轴下方.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
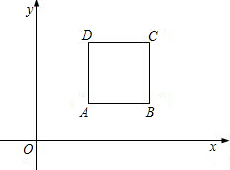 如图,四边形ABCD是正方形,已知A(5,4),B(10,4):
如图,四边形ABCD是正方形,已知A(5,4),B(10,4):