题目内容
26、学完第2章“特殊的三角形”后,老师布置了一道思考题:
如图,点M、N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.
(1)判断△ABM与△BCN是否全等,并说明理由.
(2)判断∠BQM是否会等于60°,并说明理由.

(3)若将题中的点M,N分别移动到BC,CA的延长线上,且BM=CN,是否能得到∠BQM=60°?请说明理由.

如图,点M、N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.
(1)判断△ABM与△BCN是否全等,并说明理由.
(2)判断∠BQM是否会等于60°,并说明理由.

(3)若将题中的点M,N分别移动到BC,CA的延长线上,且BM=CN,是否能得到∠BQM=60°?请说明理由.

分析:(1)因为AB=BC,∠ABM=∠BCN=60°,BM=CN,利用SAS可以证明;
(2)根据两个三角形全等,对应角相等可得∠CBN=∠BAM,∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=∠ABC=60°;
(3)和(1)同样的求法可得△ABM≌△BCN,然后利用三角形外角的性质求∠BQM=60°.
(2)根据两个三角形全等,对应角相等可得∠CBN=∠BAM,∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=∠ABC=60°;
(3)和(1)同样的求法可得△ABM≌△BCN,然后利用三角形外角的性质求∠BQM=60°.
解答:解:(1)全等,理由:
∵AB=BC,∠ABM=∠BCN=60°,BM=CN,
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠CBN=∠BAM,
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=∠ABC=60°;
(3)同(1)可证△ABM≌△BCN(SAS),
∴∠M=∠N,
∵∠QAN=∠CAM,∠BQM=∠M+∠QAN,∠ACB=∠N+∠CAM,
∴∠BQM=∠ACB=60°.
∵AB=BC,∠ABM=∠BCN=60°,BM=CN,
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠CBN=∠BAM,
∴∠BQM=∠BAM+∠ABQ=∠CBN+∠ABQ=∠ABC=60°;
(3)同(1)可证△ABM≌△BCN(SAS),
∴∠M=∠N,
∵∠QAN=∠CAM,∠BQM=∠M+∠QAN,∠ACB=∠N+∠CAM,
∴∠BQM=∠ACB=60°.
点评:此题考查了全等三角形的判定和性质,以及等边三角形的性质,综合利用了三角形外角的性质,难度中等.

练习册系列答案
相关题目
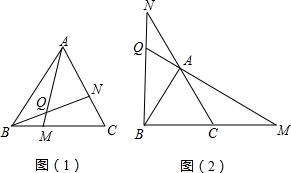 图2),且BM=CN,若∠QBM=90°,正△ABC的边长为1,试求出BQ的长.
图2),且BM=CN,若∠QBM=90°,正△ABC的边长为1,试求出BQ的长. 图2),且BM=CN,若∠QBM=90°,正△ABC的边长为1,试求出BQ的长.
图2),且BM=CN,若∠QBM=90°,正△ABC的边长为1,试求出BQ的长.