题目内容
(2012•市南区模拟)如图,已知正方形ABCD的边长与Rt△PQR的直角边PQ的长均为4cm,QR=8cm,AB与QR在同一直线l上,开始时点Q与点A重合,让△PQR以1cm/s的速度在直线l上运动,同时M点从点Q出发以1cm/s沿QP运动,直至点Q与点B重合时,都停止运动,设运动的时间为t(s),四边形PMBN的面积为S(cm2).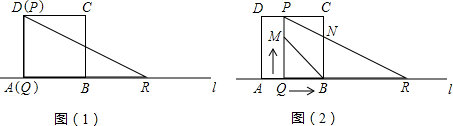
(1)当t=1s时,求S的值;
(2)求S与t之间的函数关系式,并写出自变量t的取值范围(不考虑端点);
(3)是否存在某一时刻t,使得四边形PMBN的面积S=
S△PQR?若存在,求出此时t的值;若不存在,说明理由;
(4)是否存在某一时刻t,使得四边形PMBN为平行四边形?若存在,求出此时t的值;若不存在,说明理由.
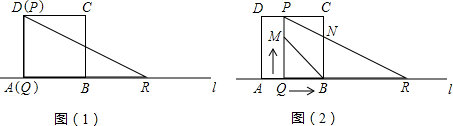
(1)当t=1s时,求S的值;
(2)求S与t之间的函数关系式,并写出自变量t的取值范围(不考虑端点);
(3)是否存在某一时刻t,使得四边形PMBN的面积S=
| 1 | 4 |
(4)是否存在某一时刻t,使得四边形PMBN为平行四边形?若存在,求出此时t的值;若不存在,说明理由.
分析:(1)当t=1时,AQ=QM=1,QB=3,BR=5,由tan∠PRQ=
就可以求出BN的值,就根据梯形面积公式就可以求出S的值;
(2)根据梯形的面积公式=
就可以表示出S的值;
(3)用(2)的结论S与t的函数关系式与S△PQR的值相等建立方程求出其解即可;
(4)根据平行四边形的判定方法当PM=BN时,求出其t的值就可以求出结论.
| PQ |
| QR |
(2)根据梯形的面积公式=
| (PM+BN)QB |
| 2 |
(3)用(2)的结论S与t的函数关系式与S△PQR的值相等建立方程求出其解即可;
(4)根据平行四边形的判定方法当PM=BN时,求出其t的值就可以求出结论.
解答:解:(1)当t=1时,AQ=MQ=1,AB=PQ=4,
∴MP=QB=4-1=3.
∵QR=8,
∴BR=8-3=5.
∵在Rt△PQR中,PQ=4,QR=8,
∴tan∠PRQ=
=
.
∴
=
,
∴
=
,
∴BN=2.5.
S四边形PMBN=
=
(0≤t≤4);
(2)由题意,得
AQ=MQ=t,PM=BQ=4-t,BR=8-(4-t)=4+t,
∴BN=2+
t,
∴S四边形PMBN=
,
=
t2-4t+12;
(3)由题意,得
t2-4t+12=
×4×8,
解得:t1=8+4
(舍去),t2=8-4
,
∴t的值为4+
;
(4)∵四边形PMBN是平行四边形,
∴PM=BN.
∵PM=4-t,BN=2+
t,
∴4-t=2+
t,
∴t=
∴t=
时,四边形PMBN为平行四边形.
∴MP=QB=4-1=3.
∵QR=8,
∴BR=8-3=5.
∵在Rt△PQR中,PQ=4,QR=8,
∴tan∠PRQ=
| PQ |
| QR |
| 1 |
| 2 |
∴
| BN |
| BR |
| 1 |
| 2 |
∴
| BN |
| 5 |
| 1 |
| 2 |
∴BN=2.5.
S四边形PMBN=
| (3+2.5)×3 |
| 2 |
| 33 |
| 4 |
(2)由题意,得
AQ=MQ=t,PM=BQ=4-t,BR=8-(4-t)=4+t,
∴BN=2+
| 1 |
| 2 |
∴S四边形PMBN=
(4-t+2+
| ||
| 2 |
=
| 1 |
| 4 |
(3)由题意,得
| 1 |
| 4 |
| 1 |
| 4 |
解得:t1=8+4
| 2 |
| 2 |
∴t的值为4+
| 2 |
(4)∵四边形PMBN是平行四边形,
∴PM=BN.
∵PM=4-t,BN=2+
| 1 |
| 2 |
∴4-t=2+
| 1 |
| 2 |
∴t=
| 4 |
| 3 |
∴t=
| 4 |
| 3 |
点评:本题是一道动点问题的综合题,考查了梯形的面积公式的运用,三角函数的正切值的运用,三角形的面积公式的运用,平行四边形的判定及性质的运用,解答时运用梯形的面积公式建立等量关系式解答本题的关键.

练习册系列答案
相关题目
 (2012•市南区模拟)如图,已知AB与⊙O相切与点C,OA=OB,⊙O的直径为8cm,AB=6cm,则OA=
(2012•市南区模拟)如图,已知AB与⊙O相切与点C,OA=OB,⊙O的直径为8cm,AB=6cm,则OA=