题目内容
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
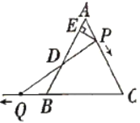
(1)若![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生变化,请说明理由.
的长;如果发生变化,请说明理由.
【答案】(1)2(2)2(3)DE=3为定值,理由见解析
【解析】
(1)根据等边三角形的性质得到∠A=60![]() ,根据三角形内角和定理得到∠APE=30
,根据三角形内角和定理得到∠APE=30![]() ,根据直角三角形的性质计算;
,根据直角三角形的性质计算;
(2)过P作PF∥QC,证明△DBQ≌△DFP,根据全等三角形的性质计算即可;
(3)根据等边三角形的性质、直角三角形的性质解答.
(1)∵△ABC是等边三角形,
∴∠A=60![]() ,
,
∵PE⊥AB,
∴∠APE=30![]() ,
,
∵AE=1,∠APE=30![]() ,PE⊥AB,
,PE⊥AB,
∴AP=2AE=2;
(2)解:过P作PF∥QC,
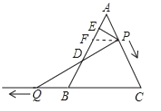
则△AFP是等边三角形,
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中,
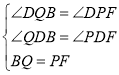 ,
,
∴△DBQ≌△DFP,
∴BD=DF,
∵∠BQD=∠BDQ=∠FDP=∠FPD=30![]() ,
,
∴BD=DF=FA=![]() AB=2,
AB=2,
∴AP=2;
(3)解:由(2)知BD=DF,
∵△AFP是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=![]() BF+
BF+![]() FA=
FA=![]() AB=3为定值,即DE的长不变.
AB=3为定值,即DE的长不变.

【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.