题目内容
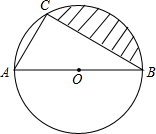 (2013•青岛)如图,AB是⊙O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是
(2013•青岛)如图,AB是⊙O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是| 4π |
| 3 |
| 3 |
| 4π |
| 3 |
| 3 |
分析:如图,连接OC.图中阴影部分的面积=扇形OBC的面积-△BOC的面积.
解答: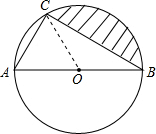 解:如图,连接OC.
解:如图,连接OC.
∵OB=OC,
∴∠OBC=∠OCB=30°
∴∠BOC=180°-30°-30°=120°.
又∵AB是直径,
∴∠ACB=90°,
∴在Rt△ABC中,AC=2,∠ABC=30°,则AB=2AC=4,BC=
=2
.
∵OC是△ABC斜边上的中线,
∴S△BOC=
S△ABC=
×
AC•BC=
×2×2
=
.
∴S阴影=S扇形OBC-S△BOC=
-
=
-
.
故答案是:
-
.
 解:如图,连接OC.
解:如图,连接OC.∵OB=OC,
∴∠OBC=∠OCB=30°
∴∠BOC=180°-30°-30°=120°.
又∵AB是直径,
∴∠ACB=90°,
∴在Rt△ABC中,AC=2,∠ABC=30°,则AB=2AC=4,BC=
| AB2-AC2 |
| 3 |
∵OC是△ABC斜边上的中线,
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 3 |
∴S阴影=S扇形OBC-S△BOC=
| 120π×22 |
| 360 |
| 3 |
| 4π |
| 3 |
| 3 |
故答案是:
| 4π |
| 3 |
| 3 |
点评:本题考查了扇形面积的计算、圆周角定理.求图中阴影部分的面积时,采用了“分割法”,即把不规则阴影图形转化为规则图形,然后来计算其面积.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
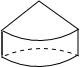 (2013•青岛)如图所示的几何体的俯视图是( )
(2013•青岛)如图所示的几何体的俯视图是( )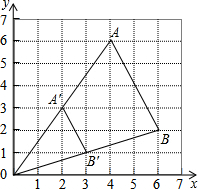 (2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
(2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )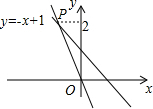 (2013•青岛)如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是
(2013•青岛)如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是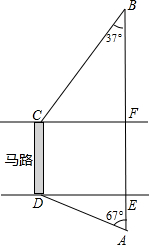 (2013•青岛)如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.
(2013•青岛)如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.