Question

【题目】小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关．因此，他们认为：可以借助物体的影子长度计算光源到物体的位置．于是，他们做了以下尝试．

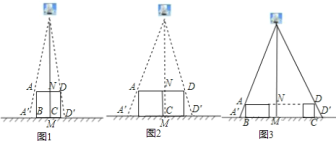
如图，垂直于地面放置的正方形框架，边长为，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子，的长度和为．那么灯泡离地面的高度为________．

不改变图中灯泡的高度，将两个边长为的正方形框架按图摆放，请计算此时横向影子，的长度和为多少？

有个边长为的正方形按图摆放，测得横向影子，的长度和为，求灯泡离地面的距离．（写出解题过程，结果用含，，的代数式表示）

Answer 1

【答案】（1）180cm；（2）；（3）．

【解析】

（1）设灯泡的位置为点P，易得△PAD∽△PA′D′，设出所求的未知数，利用相似三角形的对应边的比等于对应高的比，可得灯泡离地面的高度；

（2）同法可得到横向影子A′B，D′C的长度和；

（3）按照相应的三角形相似，利用相似三角形的对应边的比等于对应高的比，用字母表示出其他线段，即可得到灯泡离地面的距离．

设灯泡离地面的高度为，

∵，

∴，．

∴．

根据相似三角形对应高的比等于相似比的性质，可得，

∴，

解得，

故答案为：180cm；

设横向影子，的长度和为，

同理可得∴，

解得；

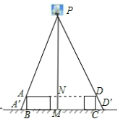
记灯泡为点，如图：

∵，∴，，

∴，

根据相似三角形对应高的比等于相似比的性质，可得，

设灯泡离地面距离为，由题意，得，，，，

∴，

，

．