题目内容
已知抛物线l1:y=-x2+2x+3和抛物线l2:y=x2+2x-3相交于A、B,其中A点的横坐标比B点的横坐标大.
(1)求A、B两点的坐标.
(2)射线OA与x轴正方向所相交成的角的正弦值.
 解:(1)解方程组
解:(1)解方程组 得
得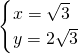 或
或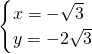 ,
,所以A点坐标为(
 ,2
,2 ),B点坐标为(-
),B点坐标为(- ,-2
,-2 );
);(2)作AH⊥x轴于H,如图,
∵A(
 ,2
,2 ),
),∴AH=2
 ,OH=
,OH=
∴tan∠AOH=
 =2,
=2,即射线OA与x轴正方向所相交成的角的正弦值等于2.
分析:(1)根据两函数图象的交点问题,得到方程组
 ,再解方程组即可得到A点坐标为(
,再解方程组即可得到A点坐标为( ,2
,2 ),B点坐标为(-
),B点坐标为(- ,-2
,-2 );
);(2)作AH⊥x轴于H,根据A点坐标得到OH=
 ,AH=2
,AH=2 ,然后根据三角形函数的定义求解.
,然后根据三角形函数的定义求解.点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
 ;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.也考查了锐角三角函数的定义.
;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.也考查了锐角三角函数的定义. 
练习册系列答案
相关题目
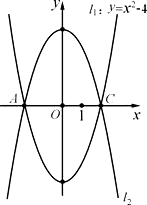 1关于x轴对称,以AC为对角线的平行四边形ABCD的第四个顶点为D.
1关于x轴对称,以AC为对角线的平行四边形ABCD的第四个顶点为D. 28、如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点,
28、如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点, l2关于P(1,3)成中心对称.
l2关于P(1,3)成中心对称.