题目内容
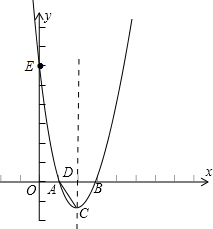
如图1,抛物线y=x2-4x+c交x轴于点A和B(-1,0)交y轴于点C,且抛物线的对称轴交x轴于点D
(1)求这个抛物线的解析式;
(2)若点E在抛物线上,且位于第四象限,当四边形ADCE面积最大时,求点E的坐标;
(3)如图2,在抛物线上是否存在这样的点P,使△PAB中的内角中有一边与x轴所夹锐角的正切值为
 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】分析:(1)依题意把点B的坐标代入函数解析式里得出c的值.
(2)连接OE,设四边形ADEF面积为S.令x=0以及y=0求出A、C的坐标.当m= 时,S有最大值.求出点E的坐标.
时,S有最大值.求出点E的坐标.
(3)本题要依靠辅助线的帮助.假设存在P点.利用三角函数求出各线段的等量关系.
解答:解:(1)∵B(-1,0)在y=x2-4x+c上,
∴(-1)2-4(-1)+c
∴c=-5
∴y=x2-4x-5 2分
(2)连接OE,由题意设四边形ADEF面积为S,
E(m,m2-4m-5)(0<m<5)3分
∵y=x2-4x-5
∴对称轴为直线x=2
∴D(2,0),DO=2
令x=0,得y=-5,
令y=0,得x1=-1,x2=5
∴A(5,0),C(0,-5)
∴AO=CO=5 4分
∴S=S四边形AOCE-S△COD=S△COE+S△AOF-S△COD= CO|xE|-
CO|xE|- AO|yE|-
AO|yE|- CO.DO
CO.DO
=- m2+
m2+ m+
m+
即S=- (m-
(m- )2+
)2+ (0<m<5)5分
(0<m<5)5分
∴当m= 时,Smax=
时,Smax=
此时m2-4m-5=-
E( ) 6分
) 6分
(3)(I)存在P1( ),P2(
),P2( ),P3(
),P3( ),P4(
),P4( )
)
(II)理由:假设存在P(m,m2-4m-5)
由题意得,tan∠PBA= 或tan∠PAB=
或tan∠PAB=
①当tan∠PBA= ,且P在第一象限时(如图2)
,且P在第一象限时(如图2)
过P点作PH⊥x轴于H
∵tan∠PBA=
∴BH=2PH,
又P(m,m2-4m-5)(m>0,m2-4m-5>0)
B(-1,0)
∴BH=m+1,PH=m2-4m-5
∴m+1=2(m2-4m-5)
∴m1=-1(舍) m2=
此时m2-4m-5=
∴P1( )7分
)7分
②当tan∠PBA= ,且P在第一象限时(如图2)
,且P在第一象限时(如图2)
与①同理BH=2PH,BH=m+1,PH=-(m2-4m-5)
∴m+1=-2(m2-4m-5)
∴m1=-1(舍) m2=
此时m2-4m-5=
∴p2( )8分
)8分
③当tan∠PBA= ,且P在第二象限时(如图3)
,且P在第二象限时(如图3)
过点P作PK⊥x轴于K
∵tan∠PBA= =
= ,
,
AK=2PK
∴AK=5-m,PK=m2-4m-5
∴5-m=2(m2-4m-5)
∴m1=5(舍) m2=
此时m2-4m-5=
∴P3( )9分
)9分
④当tan∠PBA= ,且P在第三象限时(如图3)
,且P在第三象限时(如图3)
与③同理:AK=2PK,AK=5-m,PK=-(m2-4m-5)
∴5-m=-(m2-4m-5)
∴m1=5(舍) m2=
此时m2-4m-5=
∴p4( )
)
故存在P1( ),p2(
),p2( ),P3(
),P3( ),p4(
),p4( ).10分
).10分
点评:本题难度较大.考查的是三角函数的有关知识点,二次函数的灵活运用.
(2)连接OE,设四边形ADEF面积为S.令x=0以及y=0求出A、C的坐标.当m=
 时,S有最大值.求出点E的坐标.
时,S有最大值.求出点E的坐标.(3)本题要依靠辅助线的帮助.假设存在P点.利用三角函数求出各线段的等量关系.
解答:解:(1)∵B(-1,0)在y=x2-4x+c上,
∴(-1)2-4(-1)+c
∴c=-5
∴y=x2-4x-5 2分
(2)连接OE,由题意设四边形ADEF面积为S,
E(m,m2-4m-5)(0<m<5)3分
∵y=x2-4x-5
∴对称轴为直线x=2
∴D(2,0),DO=2
令x=0,得y=-5,
令y=0,得x1=-1,x2=5
∴A(5,0),C(0,-5)
∴AO=CO=5 4分
∴S=S四边形AOCE-S△COD=S△COE+S△AOF-S△COD=
 CO|xE|-
CO|xE|- AO|yE|-
AO|yE|- CO.DO
CO.DO=-
 m2+
m2+ m+
m+
即S=-
 (m-
(m- )2+
)2+ (0<m<5)5分
(0<m<5)5分∴当m=
 时,Smax=
时,Smax=
此时m2-4m-5=-

E(
 ) 6分
) 6分(3)(I)存在P1(
 ),P2(
),P2( ),P3(
),P3( ),P4(
),P4( )
)(II)理由:假设存在P(m,m2-4m-5)
由题意得,tan∠PBA=
 或tan∠PAB=
或tan∠PAB=
①当tan∠PBA=
 ,且P在第一象限时(如图2)
,且P在第一象限时(如图2)
过P点作PH⊥x轴于H
∵tan∠PBA=

∴BH=2PH,
又P(m,m2-4m-5)(m>0,m2-4m-5>0)
B(-1,0)
∴BH=m+1,PH=m2-4m-5
∴m+1=2(m2-4m-5)
∴m1=-1(舍) m2=

此时m2-4m-5=

∴P1(
 )7分
)7分②当tan∠PBA=
 ,且P在第一象限时(如图2)
,且P在第一象限时(如图2)与①同理BH=2PH,BH=m+1,PH=-(m2-4m-5)
∴m+1=-2(m2-4m-5)
∴m1=-1(舍) m2=

此时m2-4m-5=

∴p2(
 )8分
)8分③当tan∠PBA=
 ,且P在第二象限时(如图3)
,且P在第二象限时(如图3)过点P作PK⊥x轴于K
∵tan∠PBA=
 =
= ,
,AK=2PK
∴AK=5-m,PK=m2-4m-5
∴5-m=2(m2-4m-5)
∴m1=5(舍) m2=

此时m2-4m-5=

∴P3(
 )9分
)9分④当tan∠PBA=
 ,且P在第三象限时(如图3)
,且P在第三象限时(如图3)与③同理:AK=2PK,AK=5-m,PK=-(m2-4m-5)
∴5-m=-(m2-4m-5)
∴m1=5(舍) m2=

此时m2-4m-5=

∴p4(
 )
)故存在P1(
 ),p2(
),p2( ),P3(
),P3( ),p4(
),p4( ).10分
).10分点评:本题难度较大.考查的是三角函数的有关知识点,二次函数的灵活运用.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=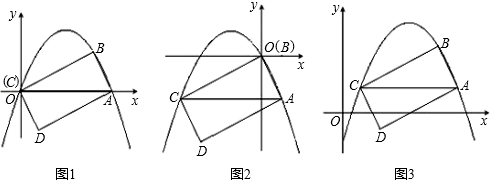
 如图,将抛物线
如图,将抛物线