题目内容
【题目】如图，对称轴为直线x= 
的抛物线经过点A（6，0）和B（0，﹣4）． 
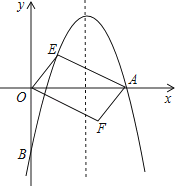
（1）求抛物线解析式及顶点坐标；
（2）设点E（x，y）是抛物线上一动点，且位于第一象限，四边形OEAF是以OA为对角线的平行四边形，求平行四边形OEAF的面积S与x之间的函数关系式；
（3）当（2）中的平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形．
【答案】
（1）
解：设抛物线的解析式为y=ax2+bx+c，
将A、B点的坐标代入函数解析式，得
，
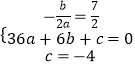解得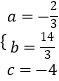 
，
抛物线的解析式为y=﹣ 
x2+ 
x﹣4，
配方，得
y=﹣ （x﹣ 
）2+ 
，
顶点坐标为（ ， ）；
（2）
解：E点坐标为（x，﹣ x2+ x﹣4），
S=2× 
OAyE=3（﹣ x2+ x﹣4）
即S=﹣2x2+14x﹣12；
（3）
解：平行四边形OEAF的面积为24时，平行四边形OEAF不能为菱形，理由如下：
当平行四边形OEAF的面积为24时，即
﹣2x2+14x﹣12=24，
化简，得
x2﹣7x+18=0，
△=b2﹣4ac=（﹣7）2﹣4×18=﹣23＜0，
方程无解，
E点不存在，
平行四边形OEAF的面积为24时，平行四边形OEAF不能为菱形
【解析】（1）根据对称轴、A、B点的坐标，可得方程，根据解方程，可得答案；
（2）根据平行四边形的面积公式，可得函数解析式；
（3）根据函数值，可得E点坐标，根据菱形的判定，可得答案．本题考查了二次函数综合题，利用待定系数法求函数解析式，配方法求函数的顶点坐标；利用平行四边形性质是解题关键；利用方程的判别式是解题关键．
阅读快车系列答案
【题目】某校倡议八年级学生利用双休日在各自社区参加义务劳动，为了解同学们劳动情况，学校随机抽查了部分学生的劳动时间，并用得到的数据绘制成不完整的统计图表，如图所示：
劳动时间（时） | 频数（人数） | 频率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.5 |
2 | 8 | y |
合计 | m | 1 |
（1）统计表中的m= ，x= ，y= ；
（2）被抽样调查的同学劳动时间的众数是 ，中位数是 ；
（3）请将条形图补充完整；
（4）求所有被调查同学的平均劳动时间．
