题目内容
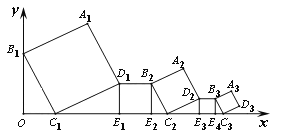
【题目】如图，在平面直角坐标系中放置了5个正方形，点B1（0，2）在y轴上，点C1，E1，E2，C2，E3，E4，C3在x轴上，C1的坐标是（1， 0），B1C1∥B2C2∥B3C3．点A3到x轴的距离是．
【答案】
【解析】
试题分析：首先根据正方形的性质构造全等三角形，利用全等三角形的性质求出点
到
轴的距离，按照同样的方法求出点
到轴的距离，根据规律求出点
到轴的距离.
试题解析：如下图所示，过点作
轴，过点
作
，
∵四边形
是正方形，
∴
，
，
∴
，
∵
，
∴
，
∴△
≌△
，
∴
，
，
∴
，
∵四边形是正方形，
可证：△≌△
，
可得：
，
∴
，
∵
∥
，
取OB1的中点S，取OC1的中点T，连接ST，易得ST∥B2C2，
∴△
≌△
，
∴
，
过点
作
轴，过点
作
，
可得：
，
，
∴
，
根据规律可得：
到
轴的距离是.
练习册系列答案
相关题目
