题目内容
已知△ABC中,∠ACB=90°(如图),点P到∠ACB两边的距离相等,且PA=PB.(1)先用尺规作出符合要求的点P(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(2)设PA=m,PC=n,试用m、n的代数式表示△ABC的周长和面积;
(3)设CP与AB交于点D,试探索当边AC、BC的长度变化时,
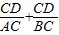 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
【答案】分析:(1)先根据角平分线及线段垂直平分线的作法作出P点,过点P分别作PE⊥AC、PF⊥CB,垂足为E、F,由全等三角形的判定定理得出Rt△APE≌Rt△BPF,再由全等三角形的性质即可判断出△ABP是等腰直角三角形;
(2)在Rt△PAB中,由∠APB=90°,PA=PB,PA=m,可得出AB= m,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得AE=BF,CE=CF,故CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中,∠PEC=90°,∠PCE=45°,PC=n,可知CE=PE=
m,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得AE=BF,CE=CF,故CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中,∠PEC=90°,∠PCE=45°,PC=n,可知CE=PE= n,即CA+CB=2CE=
n,即CA+CB=2CE= n,由△ABC的周长为=AB+BC+CA即可得出其周长,再根据S△ABC=S△PAC+S△PBC-S△PAB即可得出其面积;
n,由△ABC的周长为=AB+BC+CA即可得出其周长,再根据S△ABC=S△PAC+S△PBC-S△PAB即可得出其面积;
(3)过点D分别作DM⊥AC、DN⊥BC,垂足为M、N,由角平分线的定义及锐角三角函数的定义可知DM=DN=CDsin45°= CD,由平行线分线段成比例定理可知
CD,由平行线分线段成比例定理可知 =
=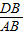 ,
, =
= ,再把两式相加即可得出结论.
,再把两式相加即可得出结论.
解答: 解:(1)依题意,点P既在∠ACB的平分线上,又在线段AB的垂直平分线上.
解:(1)依题意,点P既在∠ACB的平分线上,又在线段AB的垂直平分线上.
如图1,作∠ACB的平分线CP,作线段AB的垂直平分线PM,CP与PM的交点即为所求的P点.
△ABP是等腰直角三角形.
理由如下:过点P分别作PE⊥AC、PF⊥CB,垂足为E、F(如图2).
∵PC平分∠ACB,PE⊥AC、PF⊥CB,垂足为E、F,
∴PE=PF.
在Rt△APE与Rt△BPF中,
∵ ,
,
∴Rt△APE≌Rt△BPF.
∴∠APE=∠BPF,
∵∠PEC=90°,∠PFC=90°,∠ECF=90°,
∴∠EPF=90°,
∴∠APB=90°.
又∵PA=PB,
∴△ABP是等腰直角三角形.
(2)如图2,∵在Rt△PAB中,∠APB=90°,PA=PB,PA=m,
∴AB=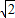 m,
m,
由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得AE=BF,CE=CF,
∴CA+CB=CE+EA+CB=CE+CF=2CE,
在Rt△PCE中,∠PEC=90°,∠PCE=45°,PC=n,
∴CE=PE= n,
n,
∴CA+CB=2CE= n,
n,
∴△ABC的周长为=AB+BC+CA= m+
m+ n.
n.
∵S△ABC=S△PAC+S△PBC-S△PAB
= AC•PF+
AC•PF+ BC•PF-
BC•PF- PA•PB
PA•PB
= (AC+BC)•PE-
(AC+BC)•PE- PA2
PA2
= ×
× n×
n× n-
n- m2
m2
= n2-
n2- m2(n>m).
m2(n>m).
[或 S△ABC= AC•BC=
AC•BC= [(AC+BC)2-(AC2+BC2)]=
[(AC+BC)2-(AC2+BC2)]= (n2-m2)]
(n2-m2)]
(3)不变.
【法1】过点D分别作DM⊥AC、DN⊥BC,垂足为M、N(图3).
易得 DM=DN=CDsin45°= CD,
CD,
由DN∥AC得 =
= ①;
①;
由DM∥BC得 =
= ②,
②,
①+②,得 +
+ =
= ,即
,即 +
+ =1
=1
∴ (
( +
+ )=1,即
)=1,即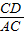 +
+ =
= ;
;
【法2】(前面同法1)又∵S△ABC=S△ACD+S△BCD,S△ABC= AC•BC
AC•BC
∴S△ACD=S△BCD= AC•DM+
AC•DM+ BC•DN=
BC•DN= (AC+BC)•
(AC+BC)• CD
CD
∴ (AC+BC)•
(AC+BC)• CD=
CD= AC•BC
AC•BC
∴ =
= ,即
,即 +
+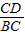 =
= ;
;
 【法3】过点D作DN⊥BC,垂足为N(图4).
【法3】过点D作DN⊥BC,垂足为N(图4).
在Rt,CDN中,∠DCN=45°,DN=CN= CD,
CD,
由DN∥AC得 =
= ①;
①; =
= ②
②
①+②,得 +
+ =
= ,即
,即 +
+ =1
=1
则 (
( +
+ )=1,即
)=1,即 +
+ =
= ;
;
【法4】过点B作BG∥DC,交射线AC于点G(如图5)
易得∠G=∠ACD=∠BCD=∠CBG=45°,BG= BC=
BC= CG.
CG.
∵BG∥DC,
∴ =
= ,
,
∴ =
= ,
, =
= ,
,
即 +
+ =
= ;
;
 【法5】过点A作CB的平行线,交射线CD于点K(见图6),
【法5】过点A作CB的平行线,交射线CD于点K(见图6),
得CK= AC,DK=CK-CD=
AC,DK=CK-CD= AC-CD,
AC-CD,
又 =
= ,即
,即 =
= ,
,
所以 =
= -
- ,即
,即 +
+ =
= ;
;
【法6】分别过点A、B分别作CD的平行线,交射线BC于点H,交射线AC于点G(见图7).
得AH= AC,BG=
AC,BG= BC,
BC,
又∵ =
= ,
, =
=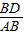
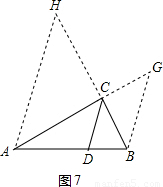
∴ +
+ =1,
=1,
即 +
+ =1,即
=1,即 +
+ =
= ;
;
点评:本题考查的是相似形综合题,涉及到角平分线及线段垂直平分线的作法及性质、平行线的性质、全等三角形的判定与性质及三角形的面积公式,涉及面较广,难度较大.
(2)在Rt△PAB中,由∠APB=90°,PA=PB,PA=m,可得出AB=
 m,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得AE=BF,CE=CF,故CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中,∠PEC=90°,∠PCE=45°,PC=n,可知CE=PE=
m,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得AE=BF,CE=CF,故CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中,∠PEC=90°,∠PCE=45°,PC=n,可知CE=PE= n,即CA+CB=2CE=
n,即CA+CB=2CE= n,由△ABC的周长为=AB+BC+CA即可得出其周长,再根据S△ABC=S△PAC+S△PBC-S△PAB即可得出其面积;
n,由△ABC的周长为=AB+BC+CA即可得出其周长,再根据S△ABC=S△PAC+S△PBC-S△PAB即可得出其面积;(3)过点D分别作DM⊥AC、DN⊥BC,垂足为M、N,由角平分线的定义及锐角三角函数的定义可知DM=DN=CDsin45°=
 CD,由平行线分线段成比例定理可知
CD,由平行线分线段成比例定理可知 =
=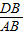 ,
, =
= ,再把两式相加即可得出结论.
,再把两式相加即可得出结论.解答:
 解:(1)依题意,点P既在∠ACB的平分线上,又在线段AB的垂直平分线上.
解:(1)依题意,点P既在∠ACB的平分线上,又在线段AB的垂直平分线上.如图1,作∠ACB的平分线CP,作线段AB的垂直平分线PM,CP与PM的交点即为所求的P点.
△ABP是等腰直角三角形.
理由如下:过点P分别作PE⊥AC、PF⊥CB,垂足为E、F(如图2).
∵PC平分∠ACB,PE⊥AC、PF⊥CB,垂足为E、F,
∴PE=PF.
在Rt△APE与Rt△BPF中,
∵
 ,
,∴Rt△APE≌Rt△BPF.
∴∠APE=∠BPF,
∵∠PEC=90°,∠PFC=90°,∠ECF=90°,
∴∠EPF=90°,
∴∠APB=90°.
又∵PA=PB,
∴△ABP是等腰直角三角形.
(2)如图2,∵在Rt△PAB中,∠APB=90°,PA=PB,PA=m,

∴AB=
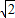 m,
m,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得AE=BF,CE=CF,
∴CA+CB=CE+EA+CB=CE+CF=2CE,
在Rt△PCE中,∠PEC=90°,∠PCE=45°,PC=n,
∴CE=PE=
 n,
n,∴CA+CB=2CE=
 n,
n,∴△ABC的周长为=AB+BC+CA=
 m+
m+ n.
n.∵S△ABC=S△PAC+S△PBC-S△PAB
=
 AC•PF+
AC•PF+ BC•PF-
BC•PF- PA•PB
PA•PB=
 (AC+BC)•PE-
(AC+BC)•PE- PA2
PA2=
 ×
× n×
n× n-
n- m2
m2=
 n2-
n2- m2(n>m).
m2(n>m).[或 S△ABC=
 AC•BC=
AC•BC= [(AC+BC)2-(AC2+BC2)]=
[(AC+BC)2-(AC2+BC2)]= (n2-m2)]
(n2-m2)](3)不变.
【法1】过点D分别作DM⊥AC、DN⊥BC,垂足为M、N(图3).

易得 DM=DN=CDsin45°=
 CD,
CD,由DN∥AC得
 =
= ①;
①;由DM∥BC得
 =
= ②,
②,①+②,得
 +
+ =
= ,即
,即 +
+ =1
=1∴
 (
( +
+ )=1,即
)=1,即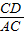 +
+ =
= ;
;【法2】(前面同法1)又∵S△ABC=S△ACD+S△BCD,S△ABC=
 AC•BC
AC•BC∴S△ACD=S△BCD=
 AC•DM+
AC•DM+ BC•DN=
BC•DN= (AC+BC)•
(AC+BC)• CD
CD∴
 (AC+BC)•
(AC+BC)• CD=
CD= AC•BC
AC•BC∴
 =
= ,即
,即 +
+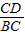 =
= ;
; 【法3】过点D作DN⊥BC,垂足为N(图4).
【法3】过点D作DN⊥BC,垂足为N(图4).在Rt,CDN中,∠DCN=45°,DN=CN=
 CD,
CD,由DN∥AC得
 =
= ①;
①; =
= ②
②①+②,得
 +
+ =
= ,即
,即 +
+ =1
=1则
 (
( +
+ )=1,即
)=1,即 +
+ =
= ;
;
【法4】过点B作BG∥DC,交射线AC于点G(如图5)
易得∠G=∠ACD=∠BCD=∠CBG=45°,BG=
 BC=
BC= CG.
CG.∵BG∥DC,
∴
 =
= ,
,∴
 =
= ,
, =
= ,
,即
 +
+ =
= ;
; 【法5】过点A作CB的平行线,交射线CD于点K(见图6),
【法5】过点A作CB的平行线,交射线CD于点K(见图6),得CK=
 AC,DK=CK-CD=
AC,DK=CK-CD= AC-CD,
AC-CD,又
 =
= ,即
,即 =
= ,
,所以
 =
= -
- ,即
,即 +
+ =
= ;
;【法6】分别过点A、B分别作CD的平行线,交射线BC于点H,交射线AC于点G(见图7).
得AH=
 AC,BG=
AC,BG= BC,
BC,又∵
 =
= ,
, =
=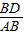

∴
 +
+ =1,
=1,即
 +
+ =1,即
=1,即 +
+ =
= ;
;点评:本题考查的是相似形综合题,涉及到角平分线及线段垂直平分线的作法及性质、平行线的性质、全等三角形的判定与性质及三角形的面积公式,涉及面较广,难度较大.

练习册系列答案
相关题目
 情况;若不可能,请说明理由.
情况;若不可能,请说明理由. 已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为
已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F 如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )
如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )