Question

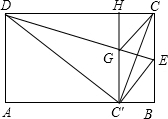已知：在矩形ABCD中，AB=2，E为BC边上的一点，沿直线DE将矩形折叠，使C点落在AB边上的C点处．过C′作C′H⊥DC，C′H分别交DE、DC于点G、H，连接CG、CC′，CC′交GE于点F．
（1）求证：四边形CGC′E为菱形；
（2）设sin∠CDE=x，并设y=

C′E+DG

DE

，试将y表示成x的函数；
（3）当（2）中所求得的函数的图象达到最高点时，求BC的长．

Answer 1

分析：（1）易得CC'被DE垂直平分，可得所求的四边形有2组邻边相等，以及一对对应角相等，利用图中的两个垂直得到C'H∥BC，可得到一对内错角相等，利用等边对等角，得到C′G=C′E，那么可得4条边相等，那么是菱形．
（2）给出了y的基本形式，那么可设分母中的单独的一个字母为未知量，其他线段用这条线段以及相应的x表示．
（3）函数图象达到最高点，那么应是当x=-

b

2a

时y相应的值．充分利用（2）在中的DG：DE的值，求得DE值，利用勾股定理可求得C'H的长，那么BC=C'H．

解答：（1）证明：根据题意，C、C′两点关于直线DE成轴对称，DE是线段CC′的垂直平分线，
故EC=EC′，GC=GC′，∠C′EG=∠CEG（2分）
由C′H⊥DC，BC⊥DC得：C′G∥CE，
∴∠C′GE=∠GEC，
∵∠C′EG=∠CEG，
∴∠C′GE=∠C′EG，
∴C′G=C′E，
∴C′G=C′E=EC=GC，
∴四边形CGCE为菱形．（4分）

（2）解：设DE=a，由sin∠CDE=

CE

DE

=x，
则CE=ax，又DC⊥CE，CF⊥DE，
∴△DCE∽△CFE，
∴

CE

FE

=

DE

CE

∴EF=

CE2

DE

=

(ax)2

a

=ax2（6分）
DG=DE-2EF=a-2ax²，
∴

C′E+DG

DE

=

CE+DG

DE

=

ax+a-2ax2

a

=x+1-2x2．（7分）
∴y=-2x²+x+1．（8分）

（3）解：由（2）得：y=-2x²+x+1=-2(x-

1

4

)2+

9

8

，（9分）
可见，当x=

1

4

时，此函数的图象达到最高点，此时

DG

DE

=1-2x2=1-

1

8

=

7

8

∵GH∥CE，
∴

DH

DC

=

DG

DE

=

7

8

，
由DC=2，得DH=

7

4

．（10分）
在Rt△DHC′中C′H=

DC′2-DH2

=

4- 49 16

=

15

4

．（11分）
∴BC=

15

4

．（12分）

点评：本题综合考查了菱形的判定，三角形的相似，勾股定理等知识．使用的判定为：四条边相等的四边形是菱形．