题目内容
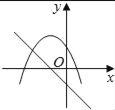
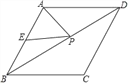
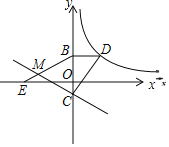
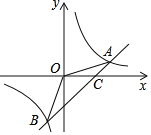
【题目】如图,一次函数y=x﹣2的图象与反比例函数y=![]() (k>0)的图象相交于A、B两点,与x轴交于点C,连接OA、OB,且tan∠AOC=
(k>0)的图象相交于A、B两点,与x轴交于点C,连接OA、OB,且tan∠AOC=![]() .
.
(1)求反比例函数的解析式;
(2)D是y轴上一点,且△BOD是以OB为腰的等腰三角形,请你求出所有符合条件的D点的坐标.
【答案】(1)![]() ;(2)点D坐标为(0,
;(2)点D坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() )或(0,﹣6).
)或(0,﹣6).
【解析】
如图,作AE⊥OC于E, 由![]() ,可以假设
,可以假设![]() ,可得
,可得![]() ,再利用待定系数法即可解决问题.
,再利用待定系数法即可解决问题.
(2)分两种情况分别求解即可解决问题.
解:(1)如图,作AE⊥OC于E.

∵![]() ,
,
∴可以假设![]() ,
,
∴![]() ,
,
∵点A在直线![]() 上,
上,
∴![]() ,
,
∴a=1,
∴A(3,1),
把A(3,1)代入![]() 上,
上,
∴![]() ,
,
∴![]() .
.
(2)由 ,解得
,解得![]() ,
,
∴![]() ,
,
∴![]() ,
,
① 当![]() 时,
时,![]() ,
,
② 当![]() 时,
时,![]() ,
,
∴![]() ,
,
综上所述,满足条件的点D坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目