题目内容
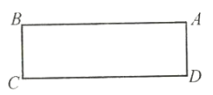
【题目】如图，在长方形
中，
，
，将长方形绕点
逆时针旋转
，点
、
、
分别对应点
、
、
.
（1）画出长方形
；
（2）联结
、
、
，请用含有
、
的代数式表示
的面积；
（3）如果交
于点
，请用含有、的代数式表示
的长度.
【答案】（1）见解析；（2）
；（3）
.
【解析】
（1）由题意知，A点旋转后对应点E正好落在边CD上，且DE=AD；线段DC的对应线段为DG，且
，所以A、D、G三点共线，确定了D、E、G三点后，过点E作CD的垂线，过点G作DG的垂线，两条垂线的交点即为B的对应点F；
（2）由旋转的性质可得FG、DG的长度，
，AB//FG，从而所求三角形的面积为
；
（3）利用
，结合（2）中所求
的面积可求出线段DH，再求CH即可.
（1）长方形
如图：
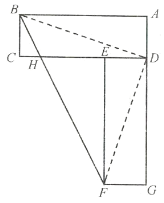
（2）由旋转图形的性质可知：
，
，
，
∴
，即
、
、
三点共线，
∴
；
（3）因为
∴
，
∴
，
所以
.
练习册系列答案
教材全解字词句篇系列答案
相关题目
