题目内容
如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )

A.b=![]() a B.b=
a B.b=![]() a C.b=
a C.b=![]() D.b=
D.b=![]() a
a
考点:
圆锥的计算。
分析:
首先利用圆锥形圣诞帽的底面周长等于侧面的弧长求得小圆的半径,然后利用两圆外切的性质求得a、b之间的关系即可.
解答:
解:∵半圆的直径为a,
∴半圆的弧长为![]()
∵把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,
∴设小圆的半径为r,则:2πr=![]()
解得:r=![]()
如图小圆的圆心为B,半圆的圆心为C,作BA⊥CA于A点,
则:AC2+AB2=BC2
即:(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2整理得:b=
)2整理得:b=![]() a
a
故选D.

点评:
本题考查了圆锥的计算,解题的关键是利用两圆相外切的性质得到两圆的圆心距,从而利用勾股定理得到a、b之间的关系.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
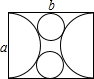 (2012•宁波)如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )
(2012•宁波)如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )
 a
a a
a
 a
a
 a
a a
a
 a
a
 a
a a
a
 a
a