Question

 

（本题12分）如图，点O是等边△ABC内一点，D是△ABC外的一点， ∠AOB= 110°，

∠BOC= 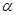，△BOC ≌△ADC，∠OCD＝60°，连接OD。

（1）求证：△OCD是等边三角形；

（2）当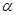＝150°时，试判断△AOD 的形状，并说明理由；

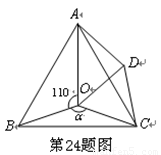
（3）探究：当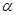为多少度时，△AOD是等腰三角形。

 

 

 

 

 

 

 

Answer 1

【答案】

（1）证明：∵△BOC≌△ADC ，

     ∴OC=DC 。——1分

     ∵∠OCD= ，

     ∴△OCD是等边三角形。——1分

（2）解：△AOD是Rt△ 。  ——1分

     理由如下：

     ∵△OCD是等边三角形 ，

     ∴∠ODC= ，

     ∵△BOC≌△ADC ，∠α= ，

     ∴∠ADC=∠BOC=∠α= ，

     ∴∠ADO=∠ADC－∠ODC=－= ，

     ∴△AOD是Rt△ 。——2分

（3）解：

    ∵△OCD是等边三角形 ，

    ∴∠COD=∠ODC=。

    ∵∠AOB= ，∠ADC=∠BOC=α ，

    ∴∠AOD=－∠AOB－∠BOC－∠COD=－－α－=－α ，

      ∠ADO=∠ADC－∠ODC=α－ ，

    ∴∠OAD=－∠AOD－∠ADO=－（－α）－（α－）= 。

    ①当∠AOD=∠ADO时，

    －α=α－ ，   ∴α= 。——2分

    ②当∠AOD=∠OAD时，

    －α= ，        ∴α= 。——2分

    ③当∠ADO=∠OAD时，

α－= ，         ∴α= 。——2分

综上所述：当α=或或时，△AOD是等腰三角形。——1分

【解析】略