题目内容
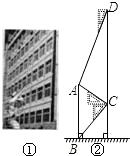 腾飞中学在教学楼前新建了一座“腾飞”雕塑(如Z图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
腾飞中学在教学楼前新建了一座“腾飞”雕塑(如Z图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据| 3 |
分析:利用题目中的仰俯角将其转化为题目直角三角形的内角,分别在Rt△ACE中和Rt△ACE中切点AC和BE 的长,两者相加即为雕塑的高.
解答: 解:过点C作CE⊥AB于E.
解:过点C作CE⊥AB于E.
∠D=90°-60°=30°,
∠ACD=90°-30°=60°,
∵CD=12,
∴AC=
CD=6.
在Rt△ACE中,
AE=AC•sin∠ACE=6×
=3;
CE=AC•cos∠ACE=6•
=3
在Rt△BCE中,
∠BCE=45°,
∴BE=CE•tan45°=3
∴AB=AE+BE=3+3
≈8.2米,
答:雕塑AB的高度约为8.2米.
 解:过点C作CE⊥AB于E.
解:过点C作CE⊥AB于E.∠D=90°-60°=30°,
∠ACD=90°-30°=60°,
∵CD=12,
∴AC=
| 1 |
| 2 |
在Rt△ACE中,
AE=AC•sin∠ACE=6×
| 1 |
| 2 |
CE=AC•cos∠ACE=6•
| ||
| 2 |
| 3 |
在Rt△BCE中,
∠BCE=45°,
∴BE=CE•tan45°=3
| 3 |
∴AB=AE+BE=3+3
| 3 |
答:雕塑AB的高度约为8.2米.
点评:本题考查了仰俯角问题,解决此类题目的关键是正确的将仰俯角转化为直角三角形的内角并用解直角三角形的知识解答即可.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
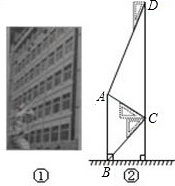 腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据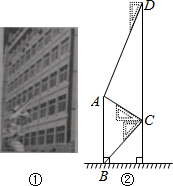 腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
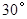 ,底部B点的俯角为
,底部B点的俯角为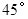 ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为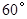 (如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确
(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确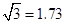 )
)