��Ŀ����
 ��ͼ������ΪD��������y=a��x-5��2-6������A��
��ͼ������ΪD��������y=a��x-5��2-6������A�� ��-5����ֱ��CD��y���ڵ�C��0��4������x���ڵ�B��
��-5����ֱ��CD��y���ڵ�C��0��4������x���ڵ�B��
��1���������ߺ�ֱ��CD����ʽ��
��2����ֱ��CD�Ҳ����������ȡ��E��ʹ�á�EDB=��CBO�������E���ꣻ
��3����PΪ����CD��һ�㣬�ڣ�2�������£�������PE����PΪ��ת������ʱ����תPE��ʹ����ת������߽�x�������ڵ�R���ҡ�EPR=��CBO���Ƿ���ڵ�R��ʹ��PE=PR��������ڣ���ֱ��д����R���ꣻ�����ڣ���˵�����ɣ�
�⣺��1������A�� ��-5������y=a��x-5��2-6��
��-5������y=a��x-5��2-6��
��-5=a�� -5��2-6�����a=
-5��2-6�����a= ��
��
���������߽���ʽΪ��y= ��x-5��2-6����y=
��x-5��2-6����y= x2-
x2-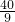 x+
x+ ��
��
��ֱ��CD����ʽΪy=kx+b��
��D��5��-6����C��0��4����
��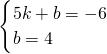 �����
����� ��
��
��ֱ��CD����ʽΪy=-2x+4��
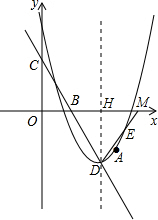 ��2���ӳ�DE��x���ڵ�M����DH��x���ڵ�H��
��2���ӳ�DE��x���ڵ�M����DH��x���ڵ�H��
�ߡ�EDB=��CBO����CBO=��MBD��
���EDB=��MBD��
��MB=MD��
���M��������t��0����
y=-2x+4����y=0ʱ��x=2��
��B��2��0����
��MB=t-2��
��Rt��DHM��MD=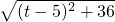 ��
��
��t-2=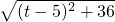 ��
��
��ã�t= ��
��
��M�� ��0����
��0����
��DM����ʽΪ��y=mx+n��
��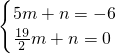 �����
�����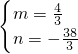 ��
��
��y= x-
x- ��
��
��EΪֱ��DM�������ߵĽ��㣬
��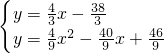 ����ã�
����ã� ��
�� ��
��
��E��8��-2����
 ��3�����ڣ���R����Ϊ��3
��3�����ڣ���R����Ϊ��3 -3��0�����������£�
-3��0�����������£�
��R��m��0����
��D��5��-6����E��8��-2����
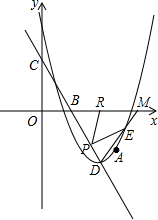
��DE=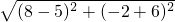 =5��
=5��
�ߡ�EPR=��CBO=��MBD��
�֡�EPR+��EPD=��MBD+��BRP��
���BRP=��EPD��
�֡�MBD=��BDE��PR=PE��
���BRP�ա�DPE��
��BP=DE=5��BR=DP��
��B��2��0����D��5��-6����
��BD= =3
=3 ��
��
��PD=BD-BP=3 -5��
-5��
��BR=PD=3 -5��
-5��
��m-2=3 -5��
-5��
��m=3 -3��
-3��
���R������3 -3��0����
-3��0����
��������1������A�� ��-5������y=a��x-5��2-6�����a=
��-5������y=a��x-5��2-6�����a= �����ɵõ������ߵĽ���ʽ����ֱ��CD����ʽΪy=kx+b����D��5��-6����C��0��4�������������룬���ô���ϵ�����������ֱ��CD�Ľ���ʽ��
�����ɵõ������ߵĽ���ʽ����ֱ��CD����ʽΪy=kx+b����D��5��-6����C��0��4�������������룬���ô���ϵ�����������ֱ��CD�Ľ���ʽ��
��2���ӳ�DE��x���ڵ�M����DH��x���ڵ�H����֤����EDB=��MBD���ó�MB=MD�����M������Ϊ��t��0��������B��2��0����D��5��-6��������t-2=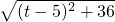 ���ⷽ�����t=
���ⷽ�����t= ���õ�M�������Ϊ��
���õ�M�������Ϊ�� ��0�������ô���ϵ�������DM�Ľ���ʽΪy=
��0�������ô���ϵ�������DM�Ľ���ʽΪy= x-
x- �����ڵ�EΪֱ��DM�������ߵĽ��㣬�ⷽ����
�����ڵ�EΪֱ��DM�������ߵĽ��㣬�ⷽ����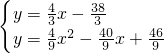 �����������E���ꣻ
�����������E���ꣻ
��3����R��m��0�����ȸ��������ľ��빫ʽ���DE=5������AAS֤����BRP�ա�DPE���ó�BP=DE=5��BR=DP���ٸ��������ľ��빫ʽ���BD=3 ����BR=PD=3
����BR=PD=3 -5����BR=DP����m-2=3
-5����BR=DP�ó�����m-2=3 -5���ⷽ�����m��ֵ���õ���R���꣬�ɴ˵ó����ۣ��ڣ�2�������£����ڵ�R���ܹ�ʹ��PE=PR��
-5���ⷽ�����m��ֵ���õ���R���꣬�ɴ˵ó����ۣ��ڣ�2�������£����ڵ�R���ܹ�ʹ��PE=PR��
�����������Ƕ��κ������ۺ����ͣ������漰�����ô���ϵ������һ�κ��������κ����Ľ���ʽ������ͼ���ϵ������������ȫ�������ε��ж������ʣ��������������������ת�����ʣ������ľ��빫ʽ��֪ʶ���ۺ��Խ�ǿ����һ���Ѷȣ��������ν�ϡ�����˼���ǽ���Ĺؼ���
 ��-5������y=a��x-5��2-6��
��-5������y=a��x-5��2-6����-5=a��
 -5��2-6�����a=
-5��2-6�����a= ��
�����������߽���ʽΪ��y=
 ��x-5��2-6����y=
��x-5��2-6����y= x2-
x2-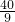 x+
x+ ��
����ֱ��CD����ʽΪy=kx+b��
��D��5��-6����C��0��4����
��
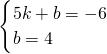 �����
����� ��
����ֱ��CD����ʽΪy=-2x+4��
 ��2���ӳ�DE��x���ڵ�M����DH��x���ڵ�H��
��2���ӳ�DE��x���ڵ�M����DH��x���ڵ�H���ߡ�EDB=��CBO����CBO=��MBD��
���EDB=��MBD��
��MB=MD��
���M��������t��0����
y=-2x+4����y=0ʱ��x=2��
��B��2��0����
��MB=t-2��
��Rt��DHM��MD=
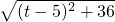 ��
����t-2=
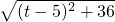 ��
����ã�t=
 ��
����M��
 ��0����
��0������DM����ʽΪ��y=mx+n��
��
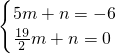 �����
�����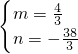 ��
����y=
 x-
x- ��
����EΪֱ��DM�������ߵĽ��㣬
��
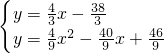 ����ã�
����ã� ��
�� ��
����E��8��-2����
 ��3�����ڣ���R����Ϊ��3
��3�����ڣ���R����Ϊ��3 -3��0�����������£�
-3��0�����������£���R��m��0����
��D��5��-6����E��8��-2����
��DE=
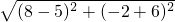 =5��
=5���ߡ�EPR=��CBO=��MBD��
�֡�EPR+��EPD=��MBD+��BRP��
���BRP=��EPD��
�֡�MBD=��BDE��PR=PE��
���BRP�ա�DPE��
��BP=DE=5��BR=DP��
��B��2��0����D��5��-6����
��BD=
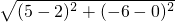 =3
=3 ��
����PD=BD-BP=3
 -5��
-5����BR=PD=3
 -5��
-5����m-2=3
 -5��
-5����m=3
 -3��
-3�����R������3
 -3��0����
-3��0���� ��������1������A��
 ��-5������y=a��x-5��2-6�����a=
��-5������y=a��x-5��2-6�����a= �����ɵõ������ߵĽ���ʽ����ֱ��CD����ʽΪy=kx+b����D��5��-6����C��0��4�������������룬���ô���ϵ�����������ֱ��CD�Ľ���ʽ��
�����ɵõ������ߵĽ���ʽ����ֱ��CD����ʽΪy=kx+b����D��5��-6����C��0��4�������������룬���ô���ϵ�����������ֱ��CD�Ľ���ʽ����2���ӳ�DE��x���ڵ�M����DH��x���ڵ�H����֤����EDB=��MBD���ó�MB=MD�����M������Ϊ��t��0��������B��2��0����D��5��-6��������t-2=
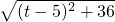 ���ⷽ�����t=
���ⷽ�����t= ���õ�M�������Ϊ��
���õ�M�������Ϊ�� ��0�������ô���ϵ�������DM�Ľ���ʽΪy=
��0�������ô���ϵ�������DM�Ľ���ʽΪy= x-
x- �����ڵ�EΪֱ��DM�������ߵĽ��㣬�ⷽ����
�����ڵ�EΪֱ��DM�������ߵĽ��㣬�ⷽ����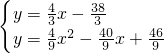 �����������E���ꣻ
�����������E���ꣻ��3����R��m��0�����ȸ��������ľ��빫ʽ���DE=5������AAS֤����BRP�ա�DPE���ó�BP=DE=5��BR=DP���ٸ��������ľ��빫ʽ���BD=3
 ����BR=PD=3
����BR=PD=3 -5����BR=DP����m-2=3
-5����BR=DP�ó�����m-2=3 -5���ⷽ�����m��ֵ���õ���R���꣬�ɴ˵ó����ۣ��ڣ�2�������£����ڵ�R���ܹ�ʹ��PE=PR��
-5���ⷽ�����m��ֵ���õ���R���꣬�ɴ˵ó����ۣ��ڣ�2�������£����ڵ�R���ܹ�ʹ��PE=PR�������������Ƕ��κ������ۺ����ͣ������漰�����ô���ϵ������һ�κ��������κ����Ľ���ʽ������ͼ���ϵ������������ȫ�������ε��ж������ʣ��������������������ת�����ʣ������ľ��빫ʽ��֪ʶ���ۺ��Խ�ǿ����һ���Ѷȣ��������ν�ϡ�����˼���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д�
�����Ŀ
 ��2013•���ݣ���ͼ����10��10�������У�ÿ��С�����DZ߳�Ϊ1��С�����Σ�ÿ��С�����εĶ����Ϊ��㣮�������߾���ͼ�е�������㣬�������������Ϊ����������γ�Ϊ�����ߵġ��ڽӸ�������Ρ�����OΪ����ԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ����������������Խ���OB����������֮��ľ���Ϊ
��2013•���ݣ���ͼ����10��10�������У�ÿ��С�����DZ߳�Ϊ1��С�����Σ�ÿ��С�����εĶ����Ϊ��㣮�������߾���ͼ�е�������㣬�������������Ϊ����������γ�Ϊ�����ߵġ��ڽӸ�������Ρ�����OΪ����ԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ����������������Խ���OB����������֮��ľ���Ϊ ��ͼ��һ�������ĺ������������Σ����ĵײ���12�ס���6�ף������ڴ���������˫��ͨ�У����涨�����������������������Ҳࡢ����·��Ե2����һ��Χ����ʻ�������ֳ��������������Ŀ�϶������
��ͼ��һ�������ĺ������������Σ����ĵײ���12�ס���6�ף������ڴ���������˫��ͨ�У����涨�����������������������Ҳࡢ����·��Ե2����һ��Χ����ʻ�������ֳ��������������Ŀ�϶������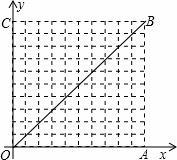
 �ף�
�ף�
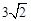 ���������������������ߵĶ����������ߵ��ڽӸ�������ε��������㣬���������������ҶԳ���ƽ����y���������������
���������������������ߵĶ����������ߵ��ڽӸ�������ε��������㣬���������������ҶԳ���ƽ����y���������������