Question

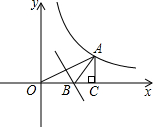如图，点A（a，b）在双曲线y=

6

x

上，a＞b＞0，OA=

13

，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为（　　）

• A、4

  7

• B、5
• C、2

  7

• D、

  22

Answer 1

分析：根据线段垂直平分线的性质可知AB=OB，由此推出△ABC的周长=OC+AC，设OC=a，AC=b，根据勾股定理和函数解析式即可得到关于a、b的方程组

ab=6 a2+b2=( 13 )2

，解之即可求出△ABC的周长．

解答：解：∵OA的垂直平分线交OC于B，
∴AB=OB，
∴△ABC的周长=OC+AC，
设OC=a，AC=b，
则有方程组

ab=6 a2+b2=( 13 )2

，
解得a+b=5，
即△ABC的周长=OC+AC=5．
故选B．

点评：本题考查反比例函数图象性质和线段中垂线性质，以及勾股定理的综合应用，关键是一个转换思想，即把求△ABC的周长转换成求OC+AC即可解决问题．