题目内容
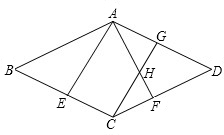
顺次连接四边形ABCD各边中点，得到四边形EFGH，要使四边形EFGH是菱形，应添加的条件是（ ）
| A．AD∥BC | B．AC=BD | C．AC⊥BD | D．AD=AB |
添加AC=BD．
如图，AC=BD，E、F、G、H分别是线段AB、BC、CD、AD的中点，
则EH、FG分别是△ABD、△BCD的中位线，EF、HG分别是△ACD、△ABC的中位线
∴EH=FG=
BD，EF=HG=
AC，
∴当AC=BD时，
EH=FG=FG=EF成立，
则四边形EFGH是菱形．
故选B．
如图，AC=BD，E、F、G、H分别是线段AB、BC、CD、AD的中点，
则EH、FG分别是△ABD、△BCD的中位线，EF、HG分别是△ACD、△ABC的中位线
∴EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴当AC=BD时，
EH=FG=FG=EF成立，
则四边形EFGH是菱形．
故选B．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
