题目内容
 二次函数y=
二次函数y=| 2 |
| 3 |
| 2 |
| 3 |
考点:二次函数的性质,二次函数图象上点的坐标特征,等边三角形的性质
专题:规律型
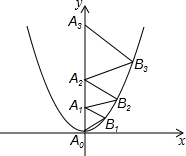
分析:根据等边三角形的性质可得∠A1A0B1=60°,然后表示出A0B1的解析式,与二次函数解析式联立求出点B1的坐标,再根据等边三角形的性质求出A0A1,同理表示出A1B2的解析式,与二次函数解析式联立求出点B2的坐标,再根据等边三角形的性质求出A1A2,同理求出B3的坐标,然后求出A2A3,从而得到等边三角形的边长为从1开始的连续自然数,与三角形所在的序数相等.
解答:解:∵△A0B1A1是等边三角形,
∴∠A1A0B1=60°,
∴A0B1的解析式为y=
x,
联立
,
解得
,
(为原点,舍去),
∴点B1(
,
),
∴等边△A0B1A1的边长为
×2=1,
同理,A1B2的解析式为y=
x+1,
联立
,
解得
,
(在第二象限,舍去),
∴B2(
,2),
∴等边△A1B2A2的边长A1A2=2×(2-1)=2,
同理可求出B3(
,
),
所以,等边△A2B3A3的边长A2A3=2×(
-1-2)=3,
…,
以此类推,系列等边三角形的边长为从1开始的连续自然数,
△A2011B2012A2012的边长A2011A2012=2012.
故答案为:2012.
∴∠A1A0B1=60°,
∴A0B1的解析式为y=
| ||
| 3 |
联立
|
解得
|
|
∴点B1(
| ||
| 2 |
| 1 |
| 2 |
∴等边△A0B1A1的边长为
| 1 |
| 2 |
同理,A1B2的解析式为y=
| ||
| 3 |
联立
|
解得
|
|
∴B2(
| 3 |
∴等边△A1B2A2的边长A1A2=2×(2-1)=2,
同理可求出B3(
3
| ||
| 2 |
| 9 |
| 2 |
所以,等边△A2B3A3的边长A2A3=2×(
| 9 |
| 2 |
…,
以此类推,系列等边三角形的边长为从1开始的连续自然数,
△A2011B2012A2012的边长A2011A2012=2012.
故答案为:2012.
点评:本题考查了二次函数图象上点的坐标特征,等边三角形的性质,主要利用了联立两函数解析式求交点坐标,根据点B系列的坐标求出等边三角形的边长并且发现系列等边三角形的边长为从1开始的连续自然数是解题的关键.

练习册系列答案
相关题目
下列说法中错误的是( )
| A、9的算术平方根是3 | ||
B、
| ||
| C、27的立方根为±3 | ||
| D、立方根等于1的数是1 |
下列说法中,错误的是( )
| A、64的立方根是4 | ||||
B、
| ||||
C、
| ||||
| D、125的立方根是±5 |
下列四个汽车标志图案中,轴对称图形是( )
A、 |
B、 |
C、 |
D、 |
下列说法,不正确的是( )
| A、0没有倒数 |
| B、0是最小的整数 |
| C、0既不是正数,也不是负数 |
| D、0是最大的非正有理数 |
下列四组线段中,可以构成直角三角形的是( )
| A、a=10,b=20,c=30 |
| B、a=20,b=30,c=40 |
| C、a=30,b=40,c=50 |
| D、a=40,b=50,c=60 |