Question

解方程组：．

Answer 1

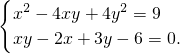解：\begin{cases} {x²-4xy+4y²=9(1)} \\ {xy-2x+3y-6=0．(2)} \end{cases}由（1）得x-2y=±3，由（2）得x+3=0，y-2=0，原方程组可化为\begin{cases} {x-2y=3} \\ {x+3=0} \end{cases}，\begin{cases} {x-2y=3} \\ {y-2=0} \end{cases}，\begin{cases} {x-2y=-3} \\ {x+3=0} \end{cases}，\begin{cases} {x-2y=-3} \\ {y-2=0.} \end{cases}解得原方程组的解为\begin{cases} {x_{1}=-3} \\ {y_{1}=-3} \end{cases}，\begin{cases} {x_{2}=7} \\ {y_{2}=2} \end{cases}，\begin{cases} {x_{3}=-3} \\ {y_{3}=0} \end{cases}，\begin{cases} {x_{4}=1} \\ {y_{4}=2.} \end{cases}