题目内容
在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是_______________
4:3.
【考点】角平分线的性质.
【分析】估计角平分线的性质,可得出△ABD的边AB上的高与△ACD的AC上的高相等,估计三角形的面积公式,即可得出△ABD与△ACD的面积之比等于对应边之比.
【解答】解:∵AD是△ABC的角平分线,
∴设△ABD的边AB上的高与△ACD的AC上的高分别为h1,h2,
∴h1=h2,
∴△ABD与△ACD的面积之比=AB:AC=4:3,
故答案为4:3.
【点评】本题考查了角平分线的性质,以及三角形的面积公式,熟练掌握三角形角平分线的性质是解题的关键.

练习册系列答案
相关题目

 ﹣1=
﹣1=
 无解,则m=( )
无解,则m=( ) B.
B. C.
C. D.
D.
 有意义,那么x的取值范围是__________
有意义,那么x的取值范围是__________ .
.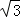 ,求BG的长.
,求BG的长.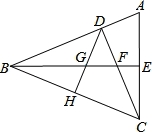
 ,
, , AD=DC,
, AD=DC, .
. 的面积.
的面积.