题目内容
在直角坐标系中,点A的坐标为(-2,0),点B的坐标为(3,0),以AB为底边,高为4的等腰三角形ABC,求点C的坐标
(
,4)或(
,-4)
| 1 |
| 2 |
| 1 |
| 2 |
(
,4)或(
,-4)
.| 1 |
| 2 |
| 1 |
| 2 |
分析:根据等腰三角形三线合一的性质求出顶点C的横坐标,再根据高的长度求出顶点C的纵坐标,即可得解.
解答: 解:∵点A的坐标为(-2,0),点B的坐标为(3,0),AB为底边,
解:∵点A的坐标为(-2,0),点B的坐标为(3,0),AB为底边,
∴顶点C的横坐标为
=
,
∵高为4,
∴顶点C的纵坐标为4或-4,
∴点C的坐标为(
,4)或(
,-4).
故答案为:(
,4)或(
,-4).
 解:∵点A的坐标为(-2,0),点B的坐标为(3,0),AB为底边,
解:∵点A的坐标为(-2,0),点B的坐标为(3,0),AB为底边,∴顶点C的横坐标为
| -2+3 |
| 2 |
| 1 |
| 2 |
∵高为4,
∴顶点C的纵坐标为4或-4,
∴点C的坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了等腰三角形的判定,等腰三角形三线合一的性质,要注意点C的坐标分两种情况,作出图形更形象直观.

练习册系列答案
相关题目
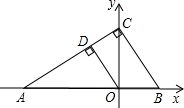 C作CB⊥AC,交x轴于B.
C作CB⊥AC,交x轴于B.