题目内容
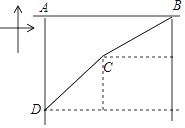
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
(1)分别写出点A的坐标 ,点B的坐标 .
(2)作出△ABC关于原点成中心对称的△A1B1C1;
(3)已知点M的坐标为(1,﹣4),请你在x轴上找一点P,使得PM+PB的值最小,并直接写出点P的坐标 .
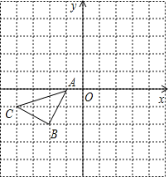
【答案】(1)A(-1,0),B(-2,-2)(2)见解析(3)(3)P(-1,0).
【解析】
(1)直接根据图形写出点A与点B的坐标;
(2)分别作出点A、点B和点C关于原点的对称点A1、B1、C1顺次连接各点即可得到图形;
(3)作M点关于x轴对称点N(1,-4),连接BN,交x轴与点P,此时|PM-PB|的值最大,求出直线NB的解析式,即可求出P点坐标.
(1)A(-1,0),B(-2,-2);
(2)作图如图1,

(3)作图如图2,

作M点关于x轴对称点N(1,-4),
连接BN,交x轴与点P,此时|PM-PB|的值最大,
根据点N(1,4),点B(2,2),
则直线NB解析式为y=-![]() x-
x-![]() ,
,
令y=0,x=-5,
则P(-5,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
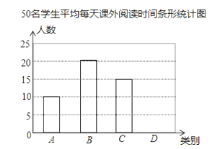
【题目】课外阅读是提高学生素养的重要途径.某校为了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间t(小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
50名学生平均每天课外阅读时间统计表
类别 | 时间t(小时) | 人数 |
A | t<0.5 | 10 |
B | 0.5≤t<1 | 20 |
C | 1≤t<1.5 | 15 |
D | t≥1.5 | a |
(1)本次调查的样本容量为多少?
(2)求表格中的a的值,并在图中补全条形统计图;
(3)该校现有1200名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?