题目内容
【题目】如图,在正方形ABCD中,E是BC上一点,BE![]() BC,连接AE,作BF⊥AE,分别与AE、CD交于点K、F,G、H分别在AD、AE上,且四边形KFGH是矩形,则
BC,连接AE,作BF⊥AE,分别与AE、CD交于点K、F,G、H分别在AD、AE上,且四边形KFGH是矩形,则![]() ________.
________.

【答案】![]()
【解析】分析:由BE![]() BC,设BE=x,则BC=3x,易证△ABE≌△BCF,得CF=BE=x,由勾股定理求出BF=
BC,设BE=x,则BC=3x,易证△ABE≌△BCF,得CF=BE=x,由勾股定理求出BF=![]() ,再证明△BKE∽△BCF,求得BK=
,再证明△BKE∽△BCF,求得BK=![]() .故HG=FK=
.故HG=FK=![]() ,从而可求出
,从而可求出![]() 的值
的值
详解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°.
∴∠BAE+∠AEB=90°
∵BF⊥AE,
∴∠BKE=90°,
∴∠KBE+∠BEK=90°,
∴∠BAE=∠KBE.
在△ABE和△BCF中,
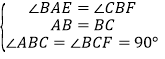
∴△ABE≌△BCF
∴CF=BE.
∵BE![]() BC,设BE=x,则BC=3x,
BC,设BE=x,则BC=3x,
∴BC=3x,CF=x,
∴BF=![]()
∵∠BKE=∠BCF=90°,∠KBE=∠CBF,
∴△BKE∽△BCF
∴![]() ,即
,即![]()
∴BK=![]()
∴KF=![]()
∵四边形KFGH是矩形,
∴GH= KF=![]()
∴![]()

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目