题目内容
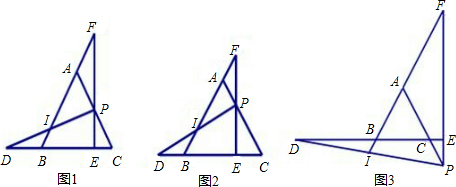
已知△ABC是等边三角形,点P是AC上一点,PE⊥BC于点E,交AB于点F,在CB的延长线上截取BD=PA,PD交AB于点I,PA=nPC.
(1)如图1,若n=1,则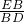 =______,
=______,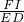 =______;
=______;
(2)如图2,若∠EPD=60°,试求n和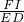 的值;
的值;
(3)如图3,若点P在AC边的延长线上,且n=3,其他条件不变,则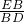 =______.(只写答案不写过程)
=______.(只写答案不写过程)
解:(1)①∵等边三角形ABC,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC,
∵EF⊥BC,
∴在直角△BEF中,∠F=30°,
∴BE= BF,
BF,
∵PA=nPC,n=1,
∴2PA=AB,
又∵∠BAC=∠F+∠APF=60°,
∴AF=AP=BD= AB,
AB,
∴BD= BF,
BF,
∵BE= BF,
BF,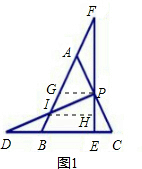
∴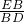 =
= ;
;
②如图1,作PG∥BC,IH∥BC,
∴IH= FI,
FI,
易证△PGI≌△DBI,则DI=PI,
∴在△PDE中,IH是中位线,
∴IH= DE,
DE,
∴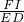 =1;
=1;
故答案为: ;1.
;1.
(2)如图2,设PC=a,则PA=an;连BP,且过P作PM⊥AB于M;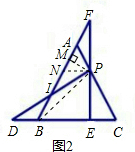
过P点作PN∥BC交AB于N,
可判断ANP为等边三角形,
所以AP=PN=AN,
∴△PNI≌△DBI(AAS),
∴IB= ,
,
又∵∠PED=90°,
∴∠D=∠BID=30°,
∴BI=BD,即 =an,
=an,
∴n= ,
,
在△AMP中可得AM=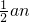 ,
,
∴BM=a+an- an=
an=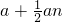 ,
,
BE=a+an- a=
a= a+an,
a+an,
又∵DB=PA,
∴DE= a+an+an=2an+
a+an+an=2an+ a,
a,
又∵∠EPC=∠APF=30°,
而∠CAF=120°,∠F=30°,
∴AF=AP=an,
∴FI=2an+ ,
,
∴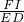 =
=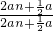 =1;
=1;
(3)∵等边三角形ABC,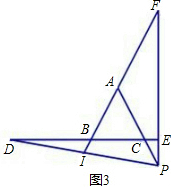
∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC,
∵EF⊥BC,
∴在直角△BEF中,∠F=30°,
∴BE= BF,
BF,
∵PA=nPC,n=3,
∴PA= AB,
AB,
又∵∠BAC=∠F+∠APF=60°,
∴AF=AP=BD= AB,
AB,
∴BD= BF,
BF,
∵BE= BF,
BF,
∴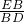 =
= .
.
故答案为:
分析:(1)①由题意,在直角△BEF中,∠F=30°,则BE= BF,又由∠BAC=∠F+∠APF=60°,可得AF=AP=BD=
BF,又由∠BAC=∠F+∠APF=60°,可得AF=AP=BD= AB,BD=
AB,BD= BF,即可得出;②如图一,作PG∥BC,IH∥BC,可得IH=
BF,即可得出;②如图一,作PG∥BC,IH∥BC,可得IH= FI,易证△PGI≌△DBI,则DI=PI,在△PDE中,IH是中位线,可得IH=
FI,易证△PGI≌△DBI,则DI=PI,在△PDE中,IH是中位线,可得IH= DE,即可得出;
DE,即可得出;
(2)连BP,且过P作PM⊥AB于M,过P点作PN∥BC交AB于N,可得ANP为等边三角形,△PNI≌△DBI(AAS),根据等边三角形的性质和全等三角形的性质,可得BI=BD,即 =an,即可得出n的值;在△AMP中可得AM=
=an,即可得出n的值;在△AMP中可得AM=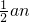 ,BM=BE=a+an-
,BM=BE=a+an- an=
an=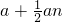 ,BE=a+an-
,BE=a+an- a=
a= a+an,由∠EPC=∠APF=30°,而∠CAF=120°,∠F=30°,则AF=AP=an,FI=2an+
a+an,由∠EPC=∠APF=30°,而∠CAF=120°,∠F=30°,则AF=AP=an,FI=2an+ ,即可求出;
,即可求出;
(3)根据(1)的推理原理,即可推出结果.
点评:本题主要考查等边三角形的性质、全等三角形的判定与性质,关键在于推出BD= AB,BD=
AB,BD= BF;推出相关三角形全等.
BF;推出相关三角形全等.
∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC,
∵EF⊥BC,
∴在直角△BEF中,∠F=30°,
∴BE=
 BF,
BF,∵PA=nPC,n=1,
∴2PA=AB,
又∵∠BAC=∠F+∠APF=60°,
∴AF=AP=BD=
 AB,
AB,∴BD=
 BF,
BF,∵BE=
 BF,
BF,
∴
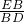 =
= ;
;②如图1,作PG∥BC,IH∥BC,
∴IH=
 FI,
FI,易证△PGI≌△DBI,则DI=PI,
∴在△PDE中,IH是中位线,
∴IH=
 DE,
DE,∴
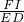 =1;
=1;故答案为:
 ;1.
;1.(2)如图2,设PC=a,则PA=an;连BP,且过P作PM⊥AB于M;

过P点作PN∥BC交AB于N,
可判断ANP为等边三角形,
所以AP=PN=AN,
∴△PNI≌△DBI(AAS),
∴IB=
 ,
,又∵∠PED=90°,
∴∠D=∠BID=30°,
∴BI=BD,即
 =an,
=an,∴n=
 ,
,在△AMP中可得AM=
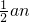 ,
,∴BM=a+an-
 an=
an=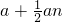 ,
,BE=a+an-
 a=
a= a+an,
a+an,又∵DB=PA,
∴DE=
 a+an+an=2an+
a+an+an=2an+ a,
a,又∵∠EPC=∠APF=30°,
而∠CAF=120°,∠F=30°,
∴AF=AP=an,
∴FI=2an+
 ,
,∴
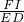 =
=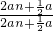 =1;
=1;(3)∵等边三角形ABC,

∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC,
∵EF⊥BC,
∴在直角△BEF中,∠F=30°,
∴BE=
 BF,
BF,∵PA=nPC,n=3,
∴PA=
 AB,
AB,又∵∠BAC=∠F+∠APF=60°,
∴AF=AP=BD=
 AB,
AB,∴BD=
 BF,
BF,∵BE=
 BF,
BF,∴
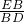 =
= .
.故答案为:

分析:(1)①由题意,在直角△BEF中,∠F=30°,则BE=
 BF,又由∠BAC=∠F+∠APF=60°,可得AF=AP=BD=
BF,又由∠BAC=∠F+∠APF=60°,可得AF=AP=BD= AB,BD=
AB,BD= BF,即可得出;②如图一,作PG∥BC,IH∥BC,可得IH=
BF,即可得出;②如图一,作PG∥BC,IH∥BC,可得IH= FI,易证△PGI≌△DBI,则DI=PI,在△PDE中,IH是中位线,可得IH=
FI,易证△PGI≌△DBI,则DI=PI,在△PDE中,IH是中位线,可得IH= DE,即可得出;
DE,即可得出;(2)连BP,且过P作PM⊥AB于M,过P点作PN∥BC交AB于N,可得ANP为等边三角形,△PNI≌△DBI(AAS),根据等边三角形的性质和全等三角形的性质,可得BI=BD,即
 =an,即可得出n的值;在△AMP中可得AM=
=an,即可得出n的值;在△AMP中可得AM=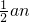 ,BM=BE=a+an-
,BM=BE=a+an- an=
an=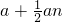 ,BE=a+an-
,BE=a+an- a=
a= a+an,由∠EPC=∠APF=30°,而∠CAF=120°,∠F=30°,则AF=AP=an,FI=2an+
a+an,由∠EPC=∠APF=30°,而∠CAF=120°,∠F=30°,则AF=AP=an,FI=2an+ ,即可求出;
,即可求出;(3)根据(1)的推理原理,即可推出结果.
点评:本题主要考查等边三角形的性质、全等三角形的判定与性质,关键在于推出BD=
 AB,BD=
AB,BD= BF;推出相关三角形全等.
BF;推出相关三角形全等. 
练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
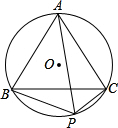 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是
 已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为
已知D是等边△ABC外一点,∠BDC=120°,则AD、BD、DC三条线段的数量关系为
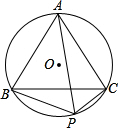 已知△ABC是等边三角形,⊙O为它的外接圆,点P是
已知△ABC是等边三角形,⊙O为它的外接圆,点P是 上任一点.
上任一点. 上任一点.
上任一点.