题目内容
已知：如图，在△ABC中，∠C＝90°，点D、E分别在边AB、AC上，DE∥BC，DE＝3， BC＝9.
（1）求
的值；
（2）若BD＝10，求sin∠A的值.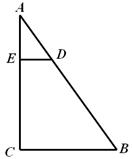
（1）求
的值；（2）若BD＝10，求sin∠A的值.
（1）
（2）
（2）解：（1）∵ DE∥BC ，∴△ADE∽△ABC。
∴＝
。
∵DE＝3， BC＝9，∴＝。
（2）∵＝，BD＝10，∴
＝。∴AD＝5。
经检验，符合题意，∴ AB＝15。
在Rt△ABC中， sin∠A＝
＝
（1）由平行线可得△ADE∽△ABC，从而由对应边成比例即可得出的值。
（2）根据（1）＝ 得出＝ ，解关于AD的方程，得出AD的值，再根据BD=10，即可求出AB的值，从而得出sin∠A的值。
∴
＝ 。∵DE＝3， BC＝9，∴
＝。（2）∵
＝，BD＝10，∴＝。∴AD＝5。经检验，符合题意，∴ AB＝15。
在Rt△ABC中， sin∠A＝
＝（1）由平行线可得△ADE∽△ABC，从而由对应边成比例即可得出
的值。（2）根据（1）
＝ 得出＝ ，解关于AD的方程，得出AD的值，再根据BD=10，即可求出AB的值，从而得出sin∠A的值。
练习册系列答案
天天向上口算本系列答案
相关题目
